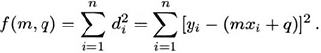Nella maggioranza delle riviste di enigmistica esiste il gioco “Unisci i puntini”.
Unendo pazientemente i vari numeri in modo sequenziale, si viene, mano a mano, a comporre una figura che la semplice sequenza di numeri non lascia intravedere facilmente, a meno di particolari abilità visive/astrattive.
Per certi aspetti, a volte il lavoro degli scienziati consiste nell’unire questi puntini ottenuti da dati sperimentali per poter interpretare i dati dell’esperimento.
In realtà, questa è una semplificazione perché nella testa di uno scienziato, prima ancora di realizzare un esperimento, c’è già un’idea (un modello/una teoria) che l’esperimento realizzato ha lo scopo di confermare o meno.
Una delle più famose dispute della storia della scienza e, in particolare, probabilmente la prima della storia della statistica, si ebbe fra i grandi matematici Gauss e Legendre e riguardava proprio l’ideazione del metodo dei minimi quadrati che, come vedremo, può essere visto come una sorta di “Unisci i puntini”.
Nel 1805, il matematico francese Adrien-Marie Legendre pubblicò un lavoro con il seguente titolo: “Nouvelles méthodes pour la détermination des orbites des comètes”[1]. In appendice a quel testo compariva la spiegazione di un metodo chiamato da Legendre «Metodo dei minimi quadrati».
In realtà, un altro grandissimo matematico, Carl Friedrich Gauss, sostenne di aver sviluppato quel metodo già in precedenza ma non lo comunicò con la stessa efficacia di Legendre[2].
A prescindere dall’attribuzione dei meriti, il metodo dei minimi quadrati, nato a partire da dati di natura astronomica, in pochi decenni si diffuse in una sempre più ampia serie di discipline.
Ovviamente questo metodo è qualcosa di molto più profondo del tracciare segmenti fra i vari punti. Il suo obiettivo è quello di trovare una funzione che meglio “descriva” i dati.
Trovata questa funzione, non solo è possibile “spiegare” i valori raccolti, ma è anche possibile fare una previsione, ovvero prevedere il valore che assume il fenomeno y in corrispondenza di un certo valore x non ancora misurato.
Per spiegare il tutto ci limiteremo ad analizzare il caso lineare, quello in cui i dati sperimentali si dispongono secondo un andamento che sembra essere quello di una retta.
Si tratta di un caso particolare, ma questa scelta dovrebbe probabilmente rendere la spiegazione più semplice. È noto inoltre che, in molti casi, l’approssimazione lineare è una delle prime vie seguite storicamente dagli scienziati alla ricerca di una prima e semplice modellizzazione di un fenomeno naturale.
In questi casi, si è soliti citare la nota frase attribuita allo statistico George Box che affermava: «All models are wrong, but some are useful» (“tutti i modelli sono sbagliati, ma alcuni sono utili”).
Fra i tanti modelli possibili, quello lineare è probabilmente il primo che uno scienziato prova (e spera) di poter applicare a un nuovo fenomeno che sta studiando.
Immaginiamo quindi di realizzare un esperimento in cui si vuole misurare il cambiamento di una grandezza Y al variare di un’altra grandezza X.
In qualche modo, nella testa di chi ha pensato l’esperimento c’è già l’idea che il fenomeno non dipenderà da altre grandezze Z,W, Q. Si cercherà inoltre di verificare se, in aggiunta a queste ipotesi, la Y dipenderà dalla X in modo lineare, ovvero attraverso la formula y= mx+q che descrive nel piano cartesiano il grafico di una generica retta. In questo caso, m è chiamato coefficiente angolare e rappresenta l’inclinazione della retta rispetto all’asse delle x e q è detto termine noto (o intercetta) e fornisce l’informazione relativa al punto in cui la retta interseca l’asse delle y.
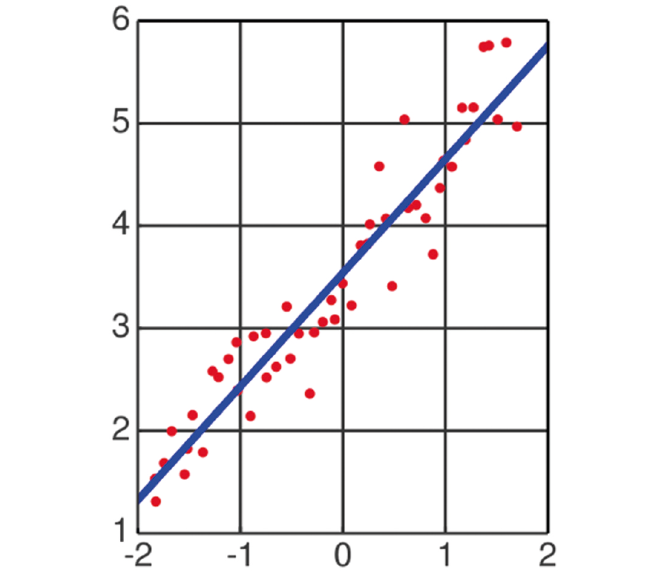
Immaginiamo di aver fatto un esperimento e di aver ottenuto i dati che sono rappresentati nel piano cartesiano dai puntini rossi, come nel caso presentato nella figura 1.
A differenza del gioco enigmistico, gli scienziati non cercheranno di unire i puntini attraverso una serie di segmenti (una cosiddetta “spezzata”) ma proveranno a tracciare un’unica retta (nella figura rappresentata in blu).
Le domande che si potranno porre per determinare questa retta sono le seguenti: quale retta va tracciata? Con che inclinazione? Dove intersecherà l’asse delle y? Deve essere una retta che passi per più punti possibili, o potrebbe non passare per nessuno dei punti tracciati?
Prima di provare a rispondere alle domande specifichiamo che, per favorire la chiarezza, stiamo semplificando il tutto utilizzando come esempio un “grafico generico” (le grandezze misurate e riportate nell’asse delle x e delle y non sono specificate). Nel grafico di esempio, inoltre, non sono riportati (cosa che invece è molto importante, in particolare per i fisici) gli errori attribuibili a ciascuna misura, o, volendo, questi errori sono così piccoli da non poter essere visti nel grafico.
Fatte queste premesse, per provare a rispondere alle domande indicate sopra, possiamo cercare, fra le infinite possibili rette descritte dalla relazione y=mx+q precedentemente introdotta, quella che passa il “più vicino possibile” alla maggioranza dei punti.
Ma cosa vuol dire “più vicino possibile”? Come si trasforma questa idea in qualcosa di matematico?
Iniziamo col dire che ogni punto rosso è rappresentato da una coppia di valori (xi, yi). Avremo quindi, per esempio, i punti (x1, y1), (x2, y2), (x3, y3) e via di seguito. Queste coppie di valori rappresentano i dati sperimentali noti. Le incognite sono, invece, i valori di m e q della retta.
La frase “il più vicino possibile” si trasforma nello scrivere per ogni punto la seguente relazione matematica:
di= yi-(mxi+q).
Il valore di rappresenta la differenza fra il generico punto yi ottenuto sperimentalmente e il valore che si otterrebbe dalla retta y=mx+q (supponendo di conoscere i valori di m e di q), inserendo al posto della generica x la xi ottenuta sperimentalmente.
La quantità che si vuole minimizzare non è quella che corrisponde a un unico punto, ma quella che considera tutti i vari dati sperimentali. Poiché, inoltre, la generica differenza di potrebbe essere sia positiva che negativa, è meglio utilizzare il suo quadrato. Per ogni punto sperimentale, si ottiene quindi un quadrato e la somma di questi termini corrisponde alla quantità che si vuole rendere minima. Utilizzando il linguaggio matematico, si ottiene una funzione che dipende dalle variabili m e q ed è data dalla somma dei quadrati di:
Per trovare i valori di m e q che rendono minima la funzione si possono usare tecniche matematiche standard (al lettore con qualche conoscenza dell’analisi sarà chiaro che in questo caso di dovrà usare lo strumento delle derivate) ma non rientra negli scopi di questo articolo divulgativo illustrare questi calcoli (per i dettagli si veda per esempio la nota 3[3]).
Nella sostanza, il risultato che si ottiene sono appunto i valori di m e di q che permettono di tracciare la retta cercata.
In un colpo solo, si è in grado quindi di rispondere a tutte le domande poste in precedenza e di individuare la “migliore” relazione lineare che lega i vari punti sperimentali.
Fra i tanti strumenti a disposizione di un ricercatore questo è probabilmente uno dei più semplici e al contempo utili. Un doveroso ringraziamento va a Gauss e Legendre che grazie a questa loro idea hanno reso possibile anche agli scienziati giocare al gioco “unisci i puntini” con i dati dei loro esperimenti.
Unendo pazientemente i vari numeri in modo sequenziale, si viene, mano a mano, a comporre una figura che la semplice sequenza di numeri non lascia intravedere facilmente, a meno di particolari abilità visive/astrattive.
Per certi aspetti, a volte il lavoro degli scienziati consiste nell’unire questi puntini ottenuti da dati sperimentali per poter interpretare i dati dell’esperimento.
In realtà, questa è una semplificazione perché nella testa di uno scienziato, prima ancora di realizzare un esperimento, c’è già un’idea (un modello/una teoria) che l’esperimento realizzato ha lo scopo di confermare o meno.
Una delle più famose dispute della storia della scienza e, in particolare, probabilmente la prima della storia della statistica, si ebbe fra i grandi matematici Gauss e Legendre e riguardava proprio l’ideazione del metodo dei minimi quadrati che, come vedremo, può essere visto come una sorta di “Unisci i puntini”.
Nel 1805, il matematico francese Adrien-Marie Legendre pubblicò un lavoro con il seguente titolo: “Nouvelles méthodes pour la détermination des orbites des comètes”[1]. In appendice a quel testo compariva la spiegazione di un metodo chiamato da Legendre «Metodo dei minimi quadrati».
In realtà, un altro grandissimo matematico, Carl Friedrich Gauss, sostenne di aver sviluppato quel metodo già in precedenza ma non lo comunicò con la stessa efficacia di Legendre[2].
A prescindere dall’attribuzione dei meriti, il metodo dei minimi quadrati, nato a partire da dati di natura astronomica, in pochi decenni si diffuse in una sempre più ampia serie di discipline.
Ovviamente questo metodo è qualcosa di molto più profondo del tracciare segmenti fra i vari punti. Il suo obiettivo è quello di trovare una funzione che meglio “descriva” i dati.
Trovata questa funzione, non solo è possibile “spiegare” i valori raccolti, ma è anche possibile fare una previsione, ovvero prevedere il valore che assume il fenomeno y in corrispondenza di un certo valore x non ancora misurato.
Per spiegare il tutto ci limiteremo ad analizzare il caso lineare, quello in cui i dati sperimentali si dispongono secondo un andamento che sembra essere quello di una retta.
Si tratta di un caso particolare, ma questa scelta dovrebbe probabilmente rendere la spiegazione più semplice. È noto inoltre che, in molti casi, l’approssimazione lineare è una delle prime vie seguite storicamente dagli scienziati alla ricerca di una prima e semplice modellizzazione di un fenomeno naturale.
In questi casi, si è soliti citare la nota frase attribuita allo statistico George Box che affermava: «All models are wrong, but some are useful» (“tutti i modelli sono sbagliati, ma alcuni sono utili”).
Fra i tanti modelli possibili, quello lineare è probabilmente il primo che uno scienziato prova (e spera) di poter applicare a un nuovo fenomeno che sta studiando.
Immaginiamo quindi di realizzare un esperimento in cui si vuole misurare il cambiamento di una grandezza Y al variare di un’altra grandezza X.
In qualche modo, nella testa di chi ha pensato l’esperimento c’è già l’idea che il fenomeno non dipenderà da altre grandezze Z,W, Q. Si cercherà inoltre di verificare se, in aggiunta a queste ipotesi, la Y dipenderà dalla X in modo lineare, ovvero attraverso la formula y= mx+q che descrive nel piano cartesiano il grafico di una generica retta. In questo caso, m è chiamato coefficiente angolare e rappresenta l’inclinazione della retta rispetto all’asse delle x e q è detto termine noto (o intercetta) e fornisce l’informazione relativa al punto in cui la retta interseca l’asse delle y.
Immaginiamo di aver fatto un esperimento e di aver ottenuto i dati che sono rappresentati nel piano cartesiano dai puntini rossi, come nel caso presentato nella figura 1.
A differenza del gioco enigmistico, gli scienziati non cercheranno di unire i puntini attraverso una serie di segmenti (una cosiddetta “spezzata”) ma proveranno a tracciare un’unica retta (nella figura rappresentata in blu).
Le domande che si potranno porre per determinare questa retta sono le seguenti: quale retta va tracciata? Con che inclinazione? Dove intersecherà l’asse delle y? Deve essere una retta che passi per più punti possibili, o potrebbe non passare per nessuno dei punti tracciati?
Prima di provare a rispondere alle domande specifichiamo che, per favorire la chiarezza, stiamo semplificando il tutto utilizzando come esempio un “grafico generico” (le grandezze misurate e riportate nell’asse delle x e delle y non sono specificate). Nel grafico di esempio, inoltre, non sono riportati (cosa che invece è molto importante, in particolare per i fisici) gli errori attribuibili a ciascuna misura, o, volendo, questi errori sono così piccoli da non poter essere visti nel grafico.
Fatte queste premesse, per provare a rispondere alle domande indicate sopra, possiamo cercare, fra le infinite possibili rette descritte dalla relazione y=mx+q precedentemente introdotta, quella che passa il “più vicino possibile” alla maggioranza dei punti.
Ma cosa vuol dire “più vicino possibile”? Come si trasforma questa idea in qualcosa di matematico?
Iniziamo col dire che ogni punto rosso è rappresentato da una coppia di valori (xi, yi). Avremo quindi, per esempio, i punti (x1, y1), (x2, y2), (x3, y3) e via di seguito. Queste coppie di valori rappresentano i dati sperimentali noti. Le incognite sono, invece, i valori di m e q della retta.
La frase “il più vicino possibile” si trasforma nello scrivere per ogni punto la seguente relazione matematica:
di= yi-(mxi+q).
Il valore di rappresenta la differenza fra il generico punto yi ottenuto sperimentalmente e il valore che si otterrebbe dalla retta y=mx+q (supponendo di conoscere i valori di m e di q), inserendo al posto della generica x la xi ottenuta sperimentalmente.
La quantità che si vuole minimizzare non è quella che corrisponde a un unico punto, ma quella che considera tutti i vari dati sperimentali. Poiché, inoltre, la generica differenza di potrebbe essere sia positiva che negativa, è meglio utilizzare il suo quadrato. Per ogni punto sperimentale, si ottiene quindi un quadrato e la somma di questi termini corrisponde alla quantità che si vuole rendere minima. Utilizzando il linguaggio matematico, si ottiene una funzione che dipende dalle variabili m e q ed è data dalla somma dei quadrati di:
Per trovare i valori di m e q che rendono minima la funzione si possono usare tecniche matematiche standard (al lettore con qualche conoscenza dell’analisi sarà chiaro che in questo caso di dovrà usare lo strumento delle derivate) ma non rientra negli scopi di questo articolo divulgativo illustrare questi calcoli (per i dettagli si veda per esempio la nota 3[3]).
Nella sostanza, il risultato che si ottiene sono appunto i valori di m e di q che permettono di tracciare la retta cercata.
In un colpo solo, si è in grado quindi di rispondere a tutte le domande poste in precedenza e di individuare la “migliore” relazione lineare che lega i vari punti sperimentali.
Fra i tanti strumenti a disposizione di un ricercatore questo è probabilmente uno dei più semplici e al contempo utili. Un doveroso ringraziamento va a Gauss e Legendre che grazie a questa loro idea hanno reso possibile anche agli scienziati giocare al gioco “unisci i puntini” con i dati dei loro esperimenti.
Note
1) A. M. Legendre, “Nouvelles méthodes pour la détermination des orbites des comètes”, disponibile qui: https://bit.ly/2PSwaP9
2) S. M. Stigler, “Gauss and the invention of least squares”, The Annals of Statistics, vol 9, No. 3, pp. 465-474, 1981.
3) M. Dapor, M. Ropele, “Elaborazione dei dati sperimentali”, Springer-Verlag, Milano 2005.