L'OMS ne spiega il significato con le seguenti parole:
«L'immunità di gregge descrive l'immunità che si ottiene quando la vaccinazione di una porzione della popolazione (il "branco") offre una protezione agli individui non protetti. La teoria dell'immunità di gregge propone che nelle malattie trasmissibili da un individuo ad un altro è difficile mantenere una catena di infezione quando un gran numero della popolazione è immune. Quindi, maggiore è la percentuale di individui immuni in una popolazione, più si riduce la probabilità che una persona suscettibile entrerà in contatto con un agente infettivo. Sia nella teoria che nella pratica, la malattia scompare di solito già prima del raggiungimento di una copertura vaccinale del 100%, questo si è visto con il vaiolo e si spera accadrà con la polio. La percentuale di individui immuni in una popolazione sopra la quale una malattia non può più persistere è la "soglia dell'immunità di gregge". Questa percentuale varia con la virulenza e la trasmissibilità di un determinato agenti infettivo, l'efficacia e la copertura complessiva del vaccino, la copertura vaccinale della popolazione a rischio e il parametro di contatto nella popolazione.»[2]
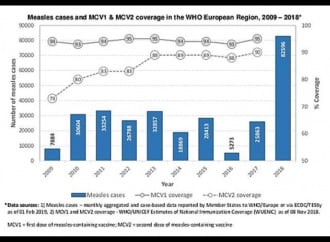
Il modello naturale dell’immunità di gregge si poteva osservare, per esempio, con l’andamento dei casi di morbillo. Nelle città, come le oscillazioni di un pendolo, il morbillo causava ogni 2-3 anni grandi epidemie mentre nel periodo tra un picco epidemico e l’altro i casi erano relativamente pochi. Ecco come si spiega questo movimento a onde. Inizialmente il virus riesce a diffondersi in modo esponenziale da un caso a diversi suscettibili (= non immuni). Mentre il numero di casi aumenta a un ritmo sempre più veloce, la proporzione dei non immuni scende gradualmente perché sempre più bambini ormai si sono ammalati e quindi non rappresentano più un obiettivo per il virus. Con il tempo, il numero medio a cui ogni malato trasmette il virus, si riduce e il numero dei nuovi casi scende. Quando il numero di immuni è tale che un caso infetta in media solo un altro soggetto, l’epidemia finisce ma il virus riesce comunque a rimanere in circolazione, in attesa che con la nascita di altri bambini la proporzione di non immuni cresca finché sarà arrivato il momento in cui un caso riesce a infettare più di un altro. Allora tutto ricomincia da capo.
In campagna e nei piccoli centri abitativi, invece, le epidemie si verificavano con intervalli più lunghi e il virus aveva anche più difficoltà a circolare tra un’epidemia e l’altra. Quando un caso genera in media meno di un nuovo caso, è la fine per il virus, che sparisce con la guarigione (o nel peggiore dei casi con la morte) del bambino. è stato osservato che al virus del morbillo, per rimanere in circolazione, serva una popolazione di almeno 400.000/500.000 abitanti (su un'isola o in una città)[3],[4].
Con le vaccinazioni si cerca quindi di raggiungere e mantenere la situazione in cui in media un malato genera meno di un altro caso, perché solo in questo modo si può spezzare la catena di trasmissione. Gli esperti di salute pubblica hanno il compito di assicurare che la percentuale di immuni sia abbastanza alta da impedire al virus di infettare uno o più di uno a partire da un caso.
Già nel diciannovesimo secolo i medici hanno notato che per far cessare i casi di vaiolo in una regione non era necessario vaccinare il 100% della popolazione.
Qui un esempio di quanto riferisce l’Ufficio Sanitario dell’Impero Tedesco, nel 1896. In Germania nel 1874 la vaccinazione contro il vaiolo è diventata obbligatoria. Una prima dose era prevista nel primo anno di vita e un richiamo nell’11° anno. Inizialmente, quando il virus ancora circolava, una parte dei bambini è stata infettata prima di ricevere la vaccinazione o la rivaccinazione. Ovviamente quelli che sono sopravvissuti non avevano più bisogno di essere vaccinati, in quanto erano già naturalmente immuni. Anno dopo anno, il numero delle coorti nate dopo la legge - e quindi vaccinate - aumentava, e il virus aveva sempre più difficoltà a circolare. Si era creato un effetto gregge che fungeva da ombrello per i bambini non immuni. Quindi i lattanti arrivavano più facilmente all’appuntamento vaccinale senza essersi ammalati nel frattempo. E gradualmente arrivavano anche più bambini al momento della rivaccinazione, senza essersi ammalati. Erano quelli che erano rimasti suscettibili dopo la prima dose oppure negli anni avevano perso parte della protezione. Questo significa che anno dopo anno, il numero di quelli esonerati perché avevano già contratto il vaiolo diminuì, grazie ad una protezione indiretta.
Il grafico dimostra che l'effetto di gregge generalmente non si forma di colpo ma gradualmente, anno dopo anno, in relazione all'aumento dei vaccinati. Allo stesso modo l'effetto di gregge diminuisce se anno dopo anno si accumulano sempre più soggetti suscettibili. In questo caso le colonne aumentano con il passare degli anni e a un certo punto scoppia un'importante epidemia. Questa non è teoria, ma è successo tante volte nel passato. Porterò degli esempi nei post successivi ciascuno dei quali sarà dedicato a una delle malattie infettive prevenibili e ai rispettivi fattori che favoriscono o ostacolano l'immunità di gregge.
Ci si può quindi immaginare che per i responsabili della Salute Pubblica è di grande interesse non solo proteggere ogni singola persona da malattie pericolose, ma anche raggiungere il più alto numero di protetti in modo che l’efficacia dei vaccini si estenda come un ombrello protettivo anche alla piccola percentuale di non immuni.
Ho preparato alcune infografiche molto semplici che servono a spiegare perché è importante superare la soglia dell'immunità di gregge calcolata per ciascuna malattia infettiva e mantenere nel tempo un'altissima percentuale di vaccinati. I miei esempi fanno anche capire perché ci possono essere casi sporadici o focolai anche in popolazioni con alta o altissima copertura vaccinale e perché questo non significa che l'immunità di gregge non esiste.
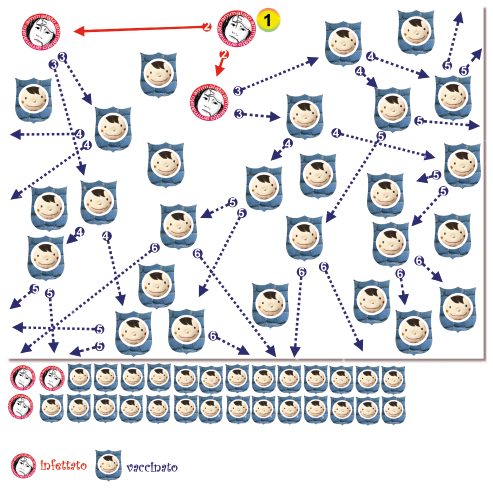
Tutti i grafici mostrano la stessa popolazione di 30 persone e i contatti tra di loro rimangono identici in ciascun'immagine. L'unica cosa che si fa è introdurre la vaccinazione e cambiare la quota e la distribuzione dei vaccinati. Così si vedrà che cosa potrebbe succedere nelle varie simulazioni quando una persona viene infettata.
Per semplificare, usiamo una malattia che (in una popolazione totalmente suscettibile) viene trasmessa da ciascun malato ad altre due persone. In epidemiologia questa grandezza viene chiamata R0 e rappresenta il numero medio di casi secondari prodotti da un’infezione primaria in una popolazione interamente suscettibile.
Quindi nel mio modello il R0 = 2. Per esempio il virus dell'ebola ha una trasmissibilità di R0 = 2. Per una malattia così poco contagiosa come quella del mio esempio, per fermare la diffusione del virus la soglia teorica dell'immunità di gregge è del 50%, cioè per fermare la diffusione dev'essere vaccinato più del 50% della popolazione. Con il virus del morbillo invece ogni malato genera da 12 a 18 nuovi casi, se viene introdotto in una comunità con zero immuni. Questo è naturalmente un valore teorico perché non esistono comunità in cui nessuno è immune al morbillo. Per fermare la trasmissione del morbillo si calcola che la percentuale minima di immuni nella popolazione dev’essere del 95% o più.
Per rendere la spiegazione più chiara, facciamo finta che ogni malato abbia contatto con due soggetti che, nel caso che non siano immuni si ammalano a loro volta e in caso di immunità (perché hanno già avuto la malattia o perché sono stati vaccinati) non si ammalano.
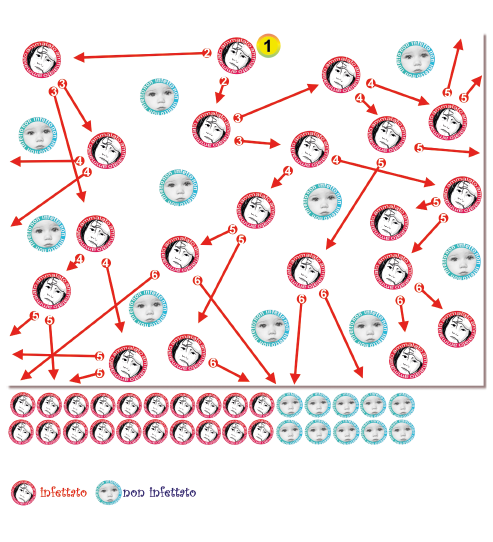
I numeri indicano le generazioni di trasmissione e insieme formano la catena di infezione. Il primo infetta due, questi due infettano a loro volta due, quindi ci saranno quattro nuovi casi di cui ciascuno infetta due, quindi abbiamo otto nuovi casi e così via.
Lascio invariati i numeri e le frecce in tutte le immagini per tenere sempre presenti i casi evitati grazie alla vaccinazione. Così si può fare un confronto con quello che sarebbe successo nella stessa popolazione senza alcuna misura di prevenzione.
Nel primo modello, su un totale di 30 persone di cui nessuna è immune, se ne ammalano 20 mentre 10 no, anche se non sono immuni. Queste vengono risparmiate perché non hanno avuto alcun contatto diretto con i casi. Ma sono salve solo per questa volta!
Potrebbero essere infettate alla prima occasione in cui vengono a contatto con un malato, per esempio nel periodo di “bassa marea” tra un picco epidemico e l’altro, oppure in una delle prossime epidemie.
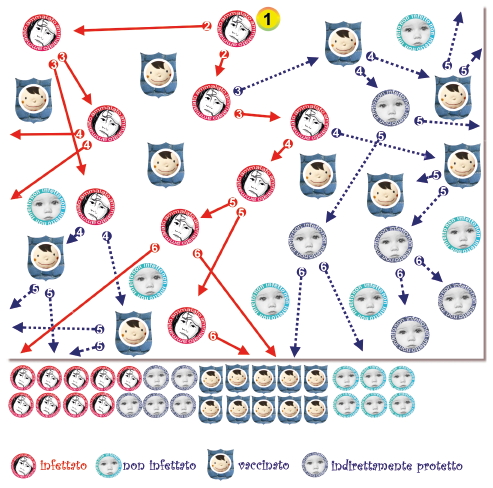
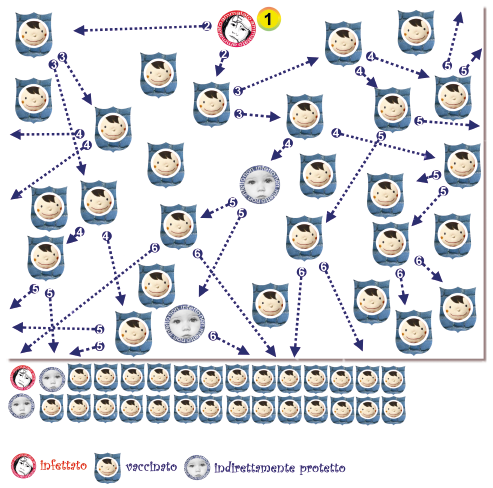
Ora prendiamo la stessa popolazione di 30 persone, ma questa volta vacciniamo 10 (il 33%) di loro e presumiamo che il vaccino abbia un’efficacia del 100% (è per semplificare perché nella vita reale nessun vaccino protegge il 100% dei soggetti; anche di questo parlerò in modo più approfondito nei successivi post). I contatti tra gli individui rimangono identici a quelli del primo grafico.
Vediamo che ancora prima di aver raggiunto la soglia dell'immunità di gregge si può notare l'effetto gregge. Nel secondo grafico solo 9 individui si sono ammalati, mentre 5 dei suscettibili, che nel primo grafico si sono ammalati, sono rimasti illesi grazie alla protezione indiretta, perché la catena di trasmissione era stata spezzata.
Ora si vaccina il 50% che è la percentuale che dovrebbe fermare le epidemie ma non eliminare del tutto la malattia.
Possiamo notare che il numero dei malati si è ulteriormente ridotto a 5 mentre quello degli indirettamente protetti è aumentato.
Vediamo anche che si è creato un sottogruppo di non vaccinati che sono in contatto tra di loro e che nonostante l'alta copertura vaccinale del resto della popolazione non hanno goduto dell'effetto gregge.
Questo è successo perché la catena di trasmissione è rimasta intatta. Se il primo fosse stato vaccinato, anche gli altri non si sarebbero ammalati, avrebbero - per questa volta almeno - approfittato dell'effetto gregge.
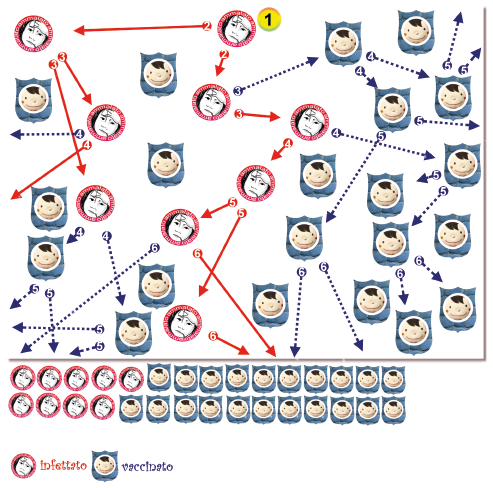
Vediamo che cosa succede se nella stessa popolazione, con gli stessi contatti si vaccinano invece 21 persone (il 70%).
In questo esempio si sono creati ben due sottogruppi (cluster) che hanno permesso al virus di diffondersi lungo la catena di trasmissione (forse nella zona si è svolto un convegno antivaccinale?).
Come vediamo, anche con una copertura vaccinale così alta esiste la possibilità che si ammalino sempre 9 persone come nell'esempio in cui il 33% è stato vaccinato.
Con i prossimi esempi lo spiego meglio.
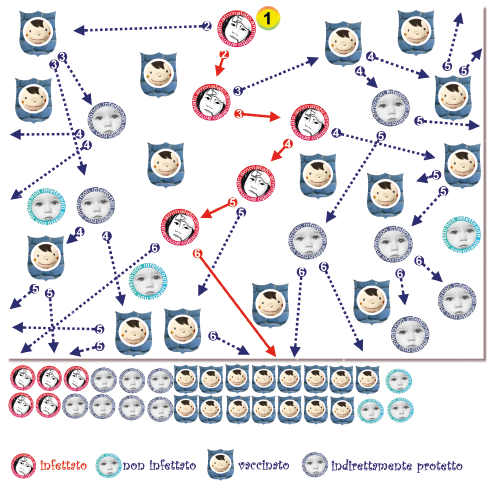
Prendiamo ancora la stessa popolazione, con gli stessi contatti e questa volta ne vacciniamo 27 (il 90%). Saremo riusciti a proteggere anche i 3 (10%) suscettibili?
Nemmeno questa volta, perché proprio quei due con cui il caso indice è venuto a contatto non erano stati vaccinati. Però la cosa importante è che la malattia si è fermata lì, perché tutti gli altri contatti erano vaccinati. Teniamo sempre in mente quante infezioni sono state evitate, guardando le frecce blu.
Vediamo ora che cosa succede, sempre vaccinando 27, quindi il 90%, ma questa volta i due contatti della seconda generazione della catena di trasmissione sono stati vaccinati (forse il convegno antivaccinale è stato rimandato...) mentre i due non vaccinati godono dell'immunità di gregge. Questo è un esempio in cui il virus viene eliminato dalla popolazione, quando il caso numero 1 sarà guarito (o morto).
Con questi esempi semplificati al massimo, si può vedere che con l'aumento del numero di vaccinati i casi sono sensibilmente diminuiti e all'agente infettivo è stata tolta l'occasione di moltiplicarsi a spese delle vittime.
Abbiamo anche visto che se un soggetto non è vaccinato viene protetto dai vaccinati che lo circondano, ma si tratta comunque di una protezione indiretta. Se dovesse entrare in contatto diretto con un malato, può essere infettato e ammalarsi, anche se tutto il resto della popolazione è vaccinato. Ma se la copertura vaccinale è alta, le probabilità di avere un contatto con un malato sono estremamente basse.
Immaginiamoci un gioco di carte nel quale perde chi pesca una carta di cuori. Se il mazzo di carte è completo, la probabilità di pescare una carta di cuori è abbastanza alta. Se si toglie la metà delle carte di cuori e le si sostituisce con altre carte (per lasciare il numero totale invariato) le probabilità si abbassano. Se se ne toglie il 90%, si dev'essere proprio sfortunati a pescare una carta di cuori, ma comunque questa possibilità rimane, visto che alcune si trovano ancora nel mazzo.
Ci sono persone, contrarie alle vaccinazioni, che usano gli sporadici casi o i piccoli focolai che si possono verificare anche in una popolazione con un'alta copertura vaccinale, per "provare" che l'immunità di gregge non esiste. Ma, come abbiamo visto, c'è una spiegazione plausibile perché ci possono essere questi casi o serie di casi. Sarebbe come dire che non ha avuto nessuna importanza sostituire con altre carte il 90% delle carte di cuori, visto che qualcuno ne ha pescata una delle poche rimaste.
Naturalmente nella vita reale la faccenda è molto più complessa, ci sono tanti fattori coinvolti e li approfondisco nei post successivi. Gli esempi che ho portato servono a spiegare il concetto su cui si basa l'immunità di gregge.
La grande preoccupazione degli esperti della Salute Pubblica per il calo della copertura vaccinale deriva anche dal fatto che questo rappresenta un altissimo numero di bambini che aumenta anno dopo anno e con il tempo saremo in una situazione ad alto rischio in cui un’importante porzione della popolazione non sarà protetta. I primi segnali di allarme li abbiamo quando scoppiano epidemie di morbillo e pertosse che sono quelle più trasmissibili. Questo ci fa capire che siamo sulla strada che ci porta a vedere con il tempo anche il ri-affacciarsi delle malattie meno trasmissibili, quindi quando con gli anni si saranno accumulati abbastanza suscettibili anche la polio e la difterite si ri-affacceranno (se nel frattempo la polio, per cui è in atto un programma di eradicazione vicinissimo al successo, non sarà stata debellata, grazie alla vaccinazione).
I bambini non vaccinati non rimangono bambini ma diventano adolescenti e adulti non vaccinati che si aggiungono a quelli che non possono essere vaccinati perché hanno una controindicazione medica, e a quella piccola percentuale di vaccinati che non hanno sviluppato l’immunità. Saranno sempre a rischio di “pescare la carta di cuori”, e il problema per loro aumenta se si tratta di malattie che possono avere gravi conseguenze se contratte da adulti (per esempio la rosolia e la varicella). Allo stesso tempo rappresentano un pericolo per tutta la società perché in caso di infezione possono trasmettere la malattia direttamente o indirettamente ad altri suscettibili, nel peggiore dei casi a qualcuno ad alto rischio di complicanze e di morte. Un bambino non vaccinato potrebbe anche diventare, quando è più grande, uno di quelli con una controindicazione permanente a un vaccino e la sua vita dipende quindi dalla vaccinazione degli altri. Se fosse stato vaccinato già da bambino, avrebbe un problema in meno.[5]
Ora si potrà anche capire perché è ritenuto poco etico il comportamento di alcuni medici che incoraggiano i genitori a rifiutare la protezione offerta dal piano vaccinale, e che sfruttano e al contempo minacciano l’immunità di gregge. Lo dimostrano le numerose affermazioni in cui questa minoranza di medici sottolinea che il calo della copertura degli ultimi anni non dovrebbe destare preoccupazione perché siamo ancora sopra la soglia ritenuta protettiva. Questa dichiarazione fa capire che in modo irresponsabile continuano a guidare i genitori che si fidano di loro verso lo sgretolamento dell’immunità di gregge e espongono a gravi rischi i loro bambini. In pratica sono indaffarati ad aggiungere sempre più carte di cuori al mazzo di carte e aumentare così la probabilità che qualcuno dei non protetti si ammali e quindi rischi personalmente di avere gravi conseguenze o che trasmetta il germe ad altri suscettibili il cui numero è in aumento per colpa della pericolosa disinformazione che viene diffusa anche da alcuni medici. Il rischio che la malattia raggiunga qualcuno che avrà dei gravi danni o muoia aumenta di pari passo al numero di non immuni.
La pericolosità di questa propaganda antivaccinale viene aggravata dal fatto che nessuno di questi medici può valutare la proporzione che potrebbe assumere l'effetto del loro operato. Che farebbero se il numero di persone che non vaccina più i figli aumentasse in modo esponenziale? Chi si prende la responsabilità di quello che potrebbe succedere in questo caso? Chi riuscirebbe a fermare questa situazione fuori controllo? Cosa direbbero ai genitori che perdono un figlio per una malattia facilmente prevenibile con le vaccinazioni?