---

Introduzione

L'editor Henry H. Bauer ha pubblicato nel numero 21.3 (ottobre 2007) del JSE una lettera scritta da Eltjo Haselhoff che commentava quest'articolo di Grassi et al..

Bauer ha presentato la lettera e ha pubblicato anche la risposta formale di Grassi et al..

Si può scaricare il file pdf originale del JSE o leggere direttamente la versione web o la sua traduzione italiana qui sotto.

Francesco Grassi, Claudio Cocheo, Paolo Russo

---

Journal of Scientific Exploration Vol. 21, n.3, pp. 576-582, 2007

Lettere al Direttore

Ancora sui cerchi nel grano

Il seguente scambio riguardante un articolo pubblicato in precedenza nel Journal of Scientific Exploration esula dalle nostre linee guida sulla lunghezza delle lettere, e in certa misura anche dalle nostre linee guida sulla concentrazione su punti specifici. Ad ogni modo, ci siamo sentiti obbligati a permettere a Haselhoff di dire la sua dopo la nostra pubblicazione di un pezzo che aveva criticato alcuni dei suoi scritti.
Avevamo pubblicato quel pezzo, come specificato all'epoca, perché la rivista che aveva diffuso il lavoro ivi commentato aveva rifiutato di accettare questo commento – in retrospettiva, si era pentita di aver dato un qualsiasi spazio alla materia dei cerchi nel grano. Il Journal of Scientific Exploration, ovviamente, è aperto proprio agli argomenti esclusi dalle sedi dell'ortodossia e crediamo anche che una rivista che ha pubblicato qualcosa dovrebbe permettere almeno una singola critica dissenziente.
Ad ogni modo, fermeremo il presente scambio a questo stadio. Qualunque futuro contributo sulla questione dei cerchi nel grano dovrà essere un articolo a tutti gli effetti e sarà sottoposto a revisione sulla base delle nostre usuali raccomandazioni circa la concentrazione, le prove presentate, l'inferenza statistica e la discussione logica.

Henry H. Bauer

Haselhoff risponde a "Sfere di luce: La scienza discutibile dei cerchi nel grano"

Vorrei commentare un articolo del vostro Giornale (Grassi, Cocheo, & Russo, 2005) che critica altri tre articoli, due dei quali scritti dal Gruppo di Ricerca BLT (Levengood 1994; Levengood & Talbott, 1999) e uno scritto da me stesso (Haselhoff, 2001). L'analisi di Grassi et al. contiene parecchi errori seri, che invalidano la maggior parte delle loro conclusioni.
Prima di tutto, Grassi et al. criticano la semplicità e mettono in dubbio la validità fisica del modello delle sfere di luce (BOL) suggerito nel mio commento (Haselhoff, 2001). Essi richiedono esplicitamente l'inclusione di meccanismi come l'assorbimento cumulativo dell'energia, effetti di umidità, riflessione, distribuzione spettrale e angolo di incidenza della presunta fonte di radiazione. Sebbene questi suggerimenti siano valide raccomandazioni per la ricerca futura, credo che non possano essere presi sul serio come critiche al mio commento, che suggeriva semplicemente una modifica alle interpretazioni del Gruppo di Ricerca BLT. L'interpretazione modificata combacia con una controparte fisica apparentemente autentica, ossia le "sfere di luce" che sono state avvistate e filmate dentro e attorno a parecchie formazioni nel grano. Inoltre, i suggerimenti di estensione del modello BOL avanzati da Grassi et al. non sono realistici perché i risultati pubblicati dal BLT (Levengood & Talbott, 1999) non si basano su esperimenti di laboratorio, svolti in un ambiente controllato, ma su un'analisi di prove indirette, sotto forma di un apparente residuo di un processo in gran parte sconosciuto. Con i dati attualmente disponibili, la realizzazione di un modello fisico avanzato come Grassi et al. suggeriscono solleverà solo più domande di quante risposte possa mai fornire.
Dopodiché, Grassi et al. (2005: p. 163) entrano in dettagli su ciò che chiamano una "discutibile strategia di campionamento". Sfortunatamente trascurano di fare una distinzione netta tra il lavoro sul campo svolto dal BLT e le verifiche aggiuntive svolte da me (usando gli stessi protocolli sul campo). I dubbi sollevati da Grassi et al. sulla scelta dei controlli, l'inclusione o esclusione degli steli verticali nell'analisi, etc., sono tutti il risultato di una profonda incomprensione del lavoro del BLT. Grassi et al. (2005: p. 165) lo dimostrano in parecchi punti del loro articolo, ad esempio quando affermano che "Nessun test statistico per confrontare le medie e le varianze ... è stato applicato", quando si tratta di una procedura standard per tutto il lavoro svolto dal BLT. Inoltre, è stato chiaramente indicato dal BLT nei loro articoli che erano stati svolti dei t-test standard, e che tutti i risultati soddisfacevano l'usuale criterio p < 0.05. Grassi et al. (2005: p. 166) dimostrano la loro scarsa conoscenza di questi argomenti nelle loro Tabelle 2a e 2b. Queste tabelle sono usate per mettere in discussione la validità statistica e il significato fisico del modello BOL, sulla base di un calcolo di valori di probabilità p (p-values, NdT). Innanzi tutto, i valori di p pubblicati in Tabella 2a per il parametro di altezza h non sono i valori per h, ma per h². E' facile capire che gli p per h² sono considerevolmente più alti. Quel che è molto peggio, tuttavia, è che tutti i valori di p pubblicati da Grassi et al. si riferiscono al caso di singole misure di lunghezza, ossia le misure di singoli nodi in varie posizioni nel campo (N = 1). Ovviamente, non era questo il caso, e perfino gli stessi Grassi et al. riportano che tutte le lunghezze dei nodi usate nell'analisi dal BLT erano valori medi di 15-20 nodi per ogni posizione nel campo, laddove – come esplicitamente riportato dal BLT nei loro articoli – tutte le variazioni di lunghezza dei nodi erano infatti statisticamente significative. Il fatto che Grassi et al. abbiano chiaramente mancato di riconoscerlo invalida tutta la loro analisi statistica, assieme alla maggior parte delle conclusioni del loro articolo.
Il punto cruciale del lavoro presentato dal BLT era la scoperta che la lunghezza dei nodi in un campo con formazioni mostra talvolta variazioni statisticamente significative (p < 0.05), geometricamente correlate alle forme impresse nel campo, sia nelle piante appiattite che in quelle in piedi. Questo rimane un risultato interessante, che tuttora credo richieda ulteriore studio. Ad ogni modo, questo fatto essenziale è stato chiaramente non compreso da Grassi et al..
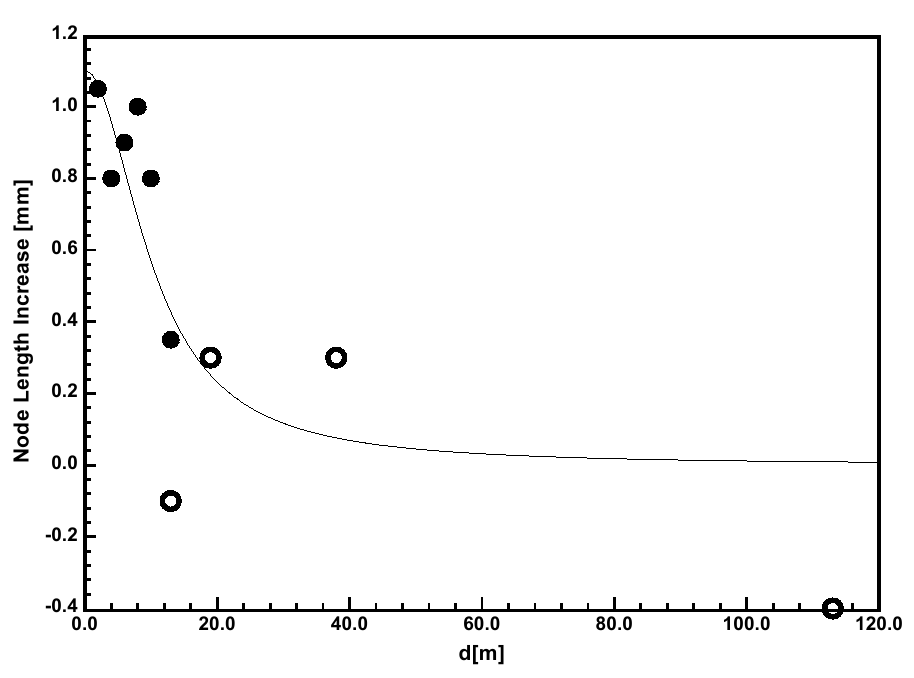
Qualche commento s'impone anche riguardo all'analisi della formazione di Nieuwerkerk da parte di Grassi et al.. I loro risultati sono basati esclusivamente su dati grezzi che ho inviato loro su richiesta. Il foglio elettronico conteneva solo numeri grezzi con un minimo di spiegazioni, ma nonostante il fatto che in seguito abbiamo comunicato parecchie volte, Grassi et al. non hanno mai discusso con me l'interpretazione dei miei dati fino a dopo il comunicato stampa che annunciava la loro pubblicazione. Come risultato, sono stati commessi alcuni sfortunati sbagli. Per esempio, le posizioni dei campioni di controllo che Grassi et al. hanno assunto, e usato nella loro analisi, erano tutte sbagliate. Una critica più rilevante riguarda invece l'esito alternativo per il coefficiente di correlazione, presentato da Grassi et al., usando i valori medi di campioni corrispondenti in due diversi insiemi radiali di campioni. Ciò non è consentito perché un tale approccio richiederebbe l'assunzione esplicita di simmetria circolare della distribuzione delle lunghezze dei nodi nel cerchio nel grano. Ovviamente, non si può fare una simile assunzione a priori perché è esattamente il punto su cui l'analisi BOL dovrebbe investigare. Successivamente, gli autori includono nell'analisi anche i campioni al di fuori dell'area appiattita nonostante siano già stati usati per la determinazione del valore di controllo (Grassi, 2006). Così fanno in modo di aumentare il coefficiente di correlazione a R² = 0.699 e concludono che la formazione di origine umana rivela caratteristiche di un cerchio nel grano "autentico". Tuttavia, l'inclusione dei dati aggiuntivi non dimostra affatto una miglior corrispondenza con il modello BOL nonostante il (modesto) incremento del coefficiente di correlazione. Questo può essere visto in Figura 1, dove i dati aggiunti da Grassi et al. sono rappresentati da cerchi vuoti. Due dei punti così aggiunti rappresentano addirittura una contrazione della lunghezza (l'aumento di lunghezza dei nodi è negativo), violando gli assunti del modello BOL. Apparentemente, il coefficiente di correlazione da solo non è un indicatore adeguato. Il ragionamento di Grassi et al. in quest'ambito non sta in piedi e non ha alcuna controparte fisica, quindi la loro conclusione non è valida. Al fine di pervenire a conclusioni solide in quest'ambito, servono più dati statistici su formazioni di origine umana, conducendo una ricerca ulteriore e originale. Questa è la base di uno studio in corso svolto da me e altri, da pubblicare più tardi in quest'anno.


Riassumendo, Grassi et al. concludono che i risultati presentati dal BLT (Levengood 1994; Levengood and Talbott, 1999) non dimostrano altro che una differenza di allungamento dei nodi tra le piante appiattite e quelle diritte, il che potrebbe essere il risultato di un qualsivoglia meccanismo di appiattimento. La loro conclusione è in linea con la loro erronea analisi statistica, per la quale ogni coppia di dati è erroneamente interpretata come il risultato di una singola misura su uno stelo. In realtà, tuttavia, tutte le variazioni riportate per la lunghezza dei nodi erano statisticamente significative, con una chiara correlazione con la forma geometrica impressa nel campo, ossia dipendente dalla distanza lineare dai cerchi. Il fatto che questo aspetto cruciale dei due articoli del BLT non sia stato riconosciuto da Grassi et al. rende invalida la maggior parte delle loro asserzioni.
Nonostante il fatto che avrei preferito una comunicazione più aperta e in particolare più onesta, vorrei ringraziare il sig. Grassi e i suoi coautori per il loro interesse nel mio lavoro. Le loro raccomandazioni saranno prese in considerazione per la ricerca futura.

Eltjo H. Haselhoff

Riferimenti

Grassi, F. (2006). Comunicazione personale.
Grassi, F., Cocheo, C., & Russo, P. (2005). Balls of light: the questionable science of crop circles. Journal of Scientific Exploration, 19(2), 159-170.
Haselhoff, E. H. (2001). Opinions and comments on Levengood WC, Talbott NP (1999). Phys. Plantarum, 111, 123-125.
Levengood, W. C. (1994). Anatomical Anomalies in Crop Formation Plants. Phys. Plantarum, 92, 356-363.
Levengood, W. C., & Talbott, N. P. (1999). Dispersion of Energies in World Wide Crop Formations. Phys. Plantarum, 105, 615-624.

La replica di Grassi, Cocheo e Russo

I commenti di Haselhoff sono i benvenuti, ma sfortunatamente non sono appropriati, come ora spiegheremo.
Sulla complessità del modello BOL: è bene fare un modello semplice, ma non è bene farlo non realistico. Un fattore può essere eliminato solo dopo che il suo impatto è stato stimato come non importante; non si può fare un'assunzione del genere senza un'analisi. In particolare, la trasparenza del tessuto alla radiazione sembra un fattore pertinente che non dovrebbe essere eliminato senza giustificazione: un tessuto perfettamente trasparente non verrebbe affatto influenzato, mentre uno stelo non trasparente schermerebbe parzialmente i suoi nodi dalla radiazione, in funzione dell'angolo di incidenza. La correttezza di un modello è indipendente dal fatto che l'ambiente sia controllato o no. E' ovvio che un modello più complesso possa richiedere più dati per essere convalidato, ma ciò può difficilmente giustificare il non farlo corretto.
Haselhoff^[1] ha già tentato di giustificare alcuni punti deboli del suo articolo sulla base del fatto che fosse un semplice commento; come abbiamo spiegato,^[2] pensiamo che non sia una giustificazione valida. E' discutibile l'uso a fini scientifici delle prove filmate e testimoniali "apparentemente autentiche" menzionate da Haselhoff a favore delle BOL. Una rassegna sarebbe fuori posto qui; forniamo solo alcuni link^[3] a dell'informazione sul solo testimone nominato nell'articolo-commento di Haselhoff così che il lettore possa giudicare quanto le sue asserzioni siano "apparentemente autentiche".
Sulla nostra presunta incomprensione dell'elaborazione dei dati del BLT e di Haselhoff: sebbene Haselhoff non sembri d'accordo, il gruppo BLT non ha mai scritto (in alcuno dei suoi articoli scientifici, quanto meno) di t-test sui dati delle formazioni di Devizes, Chehalis e del Sussex. Le asserzioni del BLT e di Haselhoff che abbiamo discusso erano basate solo su quelle tre formazioni. Il BLT ha sì menzionato dei t-test per altri dati (Beckhampton, Maryland) e questo è tutto. Ci si deve forse aspettare che noi – o chiunque altro – tiriamo a indovinare su test non pubblicati? Comunque, si dovrebbe far riferimento ai t-test per confrontare le medie dei gruppi di campioni raccolti, ma, come abbiamo chiaramente dichiarato nelle conclusioni, non abbiamo messo in dubbio la differenza media tra i campioni raccolti dentro e fuori la formazione; piuttosto, abbiamo sottolineato la mancanza di un criterio affidabile per etichettare i dati come "affetti" (dal fenomeno) o "di controllo".
Abbiamo calcolato la probabilità p per h², non per h, perché nel modello gli errori si propagano dai dati ad h², perciò è h² il termine della cui significatività occorre tenere conto. Interpretare quel termine come il quadrato (o il cubo o la potenza n-esima) di qualcos'altro non cambia la curva del modello.
E' curioso che Haselhoff indichi che abbiamo "erroneamente" trattato i dati come se fossero singoli campioni, perché è esattamente questo il modo in cui sia lui che il BLT li hanno trattati nelle loro regressioni; se avessero tenuto conto del numero e della varianza dei campioni, i coefficienti di correlazione risultanti sarebbero stati molto più bassi. Forse il risultato sarebbe stato significativo, ma sarebbe stata una significativa mancanza di correlazione. Dato che possono esistere delle motivazioni per trattare i dati nelle regressioni in quel modo, invece di sollevare un'altra obiezione il nostro obiettivo è stato solo di valutare la significatività delle loro regressioni – esattamente così com'erano. Ad ogni modo, il nostro primo commento in quest'area era (ed è) che sia il numero di cerchi presi in considerazione che il numero di campioni raccolti in ognuno sono inadeguati per un'analisi statistica affidabile; molti dei problemi specifici di cui abbiamo discusso sono solo una conseguenza.
Haselhoff travisa il lavoro suo e del BLT quando afferma che hanno solo trovato degli andamenti apparentemente non casuali e meritevoli – a loro opinione – di ulteriore studio. Prima di tutto, gli eventuali t-test menzionati da Haselhoff non supporterebbero comunque la presenza di un qualsiasi andamento, ma solo il fatto indiscusso che in ogni cerchio – comprese formazioni di origine notoriamente umana – le piante all'interno hanno nodi più lunghi di quelle all'esterno. Ma anche se l'esistenza di un generico andamento decrescente con la distanza fosse dimostrato, sarebbe una conclusione molto umile e per nulla sorprendente perché non porterebbe alcuna indicazione di una causa specifica; le possibili cause comprendono fattori ordinari come la dinamica del vento in prossimità dei bordi del cerchio e il comportamento dei circlemaker. Al contrario, i titoli dei loro articoli contengono parole come "anomalie" e "energie" e i testi vanno ben oltre. Abbiamo già replicato ai passati tentativi di Haselhoff di minimizzare.^[2]
Su Nieuwerkerk: la posizione dei campioni di controllo non è poi così sbagliata. Haselhoff^[4] ci ha mandato un file che elencava i valori dei campioni e le relative distanze dal centro di un cerchio; solo recentemente ci ha informato che i campioni di controllo erano stati presi alle distanze indicate, ma da un altro cerchio della stessa formazione. Tuttavia, a causa della simmetria della formazione, quei due cerchi erano identici sotto ogni aspetto; non c'è ragione di ipotizzare meccanismi di creazione differenti, pertanto non riusciamo ad apprezzare la pertinenza del commento di Haselhoff. Ad ogni modo, anche accettando quell'ipotesi e usando la distanza corretta dal cerchio giusto, il coefficiente di correlazione non cambia apprezzabilmente. In quanto agli altri commenti di Haselhoff sullo stesso cerchio, avrebbe ragione se avessimo mai asserito che il cerchio di Nieuwerkerk (una formazione di nota origine umana) fosse stato creato da una BOL. Ovviamente non l'abbiamo mai fatto; il nostro scopo era del tutto diverso. Le conclusioni del BLT e di Haselhoff erano basate su tre soli cerchi, ognuno dei quali campionato solo in pochi punti senza informazione bidimensionale. Inoltre, la classificazione dei campioni come "affetti" o "di controllo" sembrava arbitraria e decisa dopo aver visto i valori; non è stato tentato alcun confronto con modelli alternativi ed eventualmente più corrispondenti ai dati o fisicamente più fondati. Non è discutibile questa procedura? Non può condurre a risultati spuri apparentemente positivi? Non solo ne abbiamo spiegato i motivi, ma abbiamo aggiunto un esempio. Abbiamo preso in considerazione il noto cerchio di Nieuwerkerk di origine umana, che Haselhoff ha campionato e usato come esempio di risultato negativo, e lo abbiamo trattato allo stesso modo degli altri cerchi. Abbiamo mediato due insiemi di dati, raccolti lungo raggi differenti, sia per eliminare l'informazione bidimensionale (comunque, come conseguenza della simmetria sferica della BOL, non ci si dovrebbe aspettare alcun cambiamento variando la direzione del raggio, ma solo in funzione della distanza dal centro) che per ridurre (a sette) il numero dei campioni, in modo che non fosse disponibile più informazione su quel cerchio di quanta ve ne fosse per gli altri, al fine di consentire un confronto alla pari. Poi abbiamo aggregato i dati come affetti o di controllo in vari modi sensati, mostrando come il coefficiente di correlazione risultante venisse influenzato da una scelta arbitraria di ognuno di essi; il modo menzionato da Haselhoff era semplicemente l'ultimo. Siamo assolutamente d'accordo che il risultato apparentemente positivo che abbiamo ottenuto con pochi dati aggregati arbitrariamente non dovrebbe essere preso sul serio, ma ciò dimostra proprio il nostro punto, che a Haselhoff sembra sfuggire. Gli sfugge anche di più quando propone che se il valore di un campione è al di sotto del livello dei controlli (un'apparente "contrazione"), allora il modello dovrebbe essere respinto. Non è possibile che pensi realmente che i nodi vicini a cerchi fatti dall'uomo si contraggano davvero; si tratta solo di variabilità nei dati ed è già gestita adeguatamente dai test statistici. Ciononostante, accetteremmo la regola di Haselhoff se solo l'avesse dichiarata in anticipo; aggiustare i criteri dopo aver guardato i risultati è esattamente una delle pratiche discutibili che abbiamo criticato.
Infine, sul cerchio di Nieuwerkerk, Haselhoff conclude con l'ammissione che "apparentemente, il coefficiente di correlazione da solo non è un indicatore adeguato". Questa è esattamente la nostra critica al suo lavoro. Siamo d'accordo con lui: un coefficiente di correlazione da solo non è un indicatore adeguato. Ma è il solo indicatore usato dallo stesso Haselhoff per cercare di dimostrare l'esistenza di una BOL. Così, Haselhoff stesso ammette che tutto il suo lavoro in quest'ambito è supportato solo da un indicatore la cui adeguatezza è opinabile.
Vorremmo anche far notare che la replica di Haselhoff non accenna a parecchi dei punti che abbiamo sollevato; per esempio, l'incoerenza del meccanismo fisico proposto (dilatazione termica dell'acqua) e l'esclusione di parecchi dati dall'analisi (ciuffi centrali, cerchio di Beckhampton).
In conclusione, i commenti di Haselhoff sono i benvenuti, ma non contribuiscono a rendere più solido il suo articolo, né a invalidare le critiche che gli abbiamo rivolto.

Francesco Grassi
Claudio Cocheo
Paolo Russo

Riferimenti