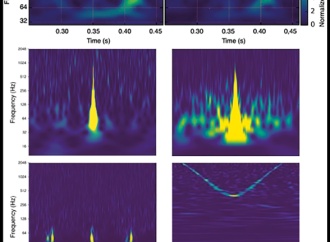
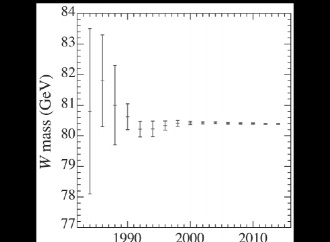
Questo è esattamente quello che accade, per esempio, se lanciamo per aria la girandola e osserviamo il suo perno fare un moto di traslazione (va a spasso) e le pale girare attorno a esso (ruotano). Il punto rappresentativo dell’oggetto, in questo caso il suo perno, è molto importante in fisica: si tratta del baricentro o, più o meno, del suo centro di massa che, per oggetti simmetrici, si trova in una posizione che non è usualmente difficile da calcolare: per una palla, per esempio, si trova nel suo centro geometrico. Questo punto ubbidisce alle leggi del moto di Newton per quello che riguarda l’effetto di forze esterne che agiscono sull’oggetto, come per esempio il suo peso. Le leggi di Newton vengono però utilizzate, in altro formato, per arrivare a descrivere anche il moto attorno al centro di massa, ovvero le rotazioni. Per descrivere una rotazione, come appena accennato, è necessario misurare la “legge oraria” (di variazione nel tempo, in pratica) di un angolo una volta specificato l’asse. Dobbiamo anche specificare il verso della rotazione, ovvero se oraria o anti-oraria. Per questo i fisici si sono messi d’accordo da molto tempo per adottare una convenzione secondo la quale una rotazione è “positiva” se è oraria vista guardando l’oggetto con l’asse di rotazione che punta dall’osservatore verso l’oggetto, e viceversa. Questa regoletta è anche nota come regola della mano destra, o del cacciavite, o del cavatappi: tutti promemoria che, a seconda dei gusti, ci aiutano a decidere se una rotazione sia positiva o negativa. Per esempio, una rotazione è vista oraria, positiva, quando il suo asse è allineato con quello di avanzamento di un cacciavite (o di un cavatappi) ruotato nel suo stesso verso, ovvero orario. Pensate al moto che si fa per avvitare e svitare o per stappare.
Ciò detto, se abbiamo rotazione, se cioè l’angolo varia, ci si può chiedere se la rotazione sia più o meno rapida. Ovvero ci si può chiedere quanto valga intuitivamente una velocità angolare: se quella di traslazione si misurava in chilometri all’ora o metri al secondo, quella di rotazione si misura ovviamente in gradi al secondo (gradi angolari, non alcolici, qui il cavatappi non c’entra in quel senso). Si potrebbe anche misurare una rotazione – e lo si fa, infatti – con unità di misura ibride, non del Sistema Internazionale, come per esempio “rotazioni al minuto” o cose simili. Ci si potrebbe poi anche chiedere come misurare eventuali variazioni di velocità angolare, esattamente come si misurano – in termini di accelerazioni – le variazioni di velocità di traslazione. Ecco che allora si può introdurre un’idea intuitiva e poi anche una pratica di accelerazione angolare: se si inizia a far ruotare una giostra da ferma per portarla alla sua velocità (angolare) di funzionamento, è ovvio che siamo al cospetto di un moto di rotazione accelerato, né più né meno di quanto accade nelle traslazioni. A questo punto la storia dovrebbe essere chiara: è importante ricordare il ruolo che delle forze hanno nel provocare variazioni di velocità di una massa e di come le equazioni della dinamica di Newton siano in grado di descrivere perfettamente questa classe di fenomeni. In generale, data l’inerzia (la massa) di un oggetto materiale e data la forza che su di esso agisce, si ottiene l’accelerazione che esso subisce secondo una legge relativamente semplice: l’accelerazione è direttamente proporzionale alla forza totale agente e la costante di proporzionalità è proprio l’inerzia al moto, la massa.
Ora, se prendiamo la nostra girandola, sempre tenendo bloccato il suo perno di modo che non vada a spasso, sappiamo benissimo come fare per mettere la girandola in moto rotazionale: spingiamo una delle sue pale agendo con una forza perpendicolarmente a essa oppure, se l’esempio ci è più chiaro, basta pensare a come facciamo a mettere in moto una piccola giostra per bambini in un parco giochi. Ci vuole una forza (spingiamo) ma questa deve essere applicata soddisfacendo due richieste essenziali: la spinta non deve essere applicata all’asse di rotazione e deve avere almeno una parte agente perpendicolarmente al segmento che collega il punto di applicazione all’asse stesso. Provare per credere in entrambi i casi: spingere una porta sui cardini o tirarla parallelamente a sé stessa non è molto furbo, a meno che non si intenda far danni. Applicare una forza con queste caratteristiche “geometriche” in fisica equivale ad applicare un “momento di forza”, detto anche “coppia” in meccanica (torque in inglese). Un momento di forza è il prodotto di una forza per il suo “braccio”, a realizzare la famosa leva che Archimede in un momento di particolare enfasi voleva usare per sollevare il mondo, pur di avere un asse di rotazione o un fulcro. Il momento si calcola tenendo conto della collocazione della forza rispetto al braccio ma, al di là di regole matematiche, quello che conta qui è che si è trovata l’estensione rotazionale della forza, cioè quella grandezza che in fisica permette la variazione di una velocità angolare, ovvero l’immissione in moto rotazionale di un corpo attorno a un asse – come pure il suo rallentamento, in caso di azione avversa del momento di forza.
Sottolineiamo la linearità del ragionamento: forza implica accelerazione con inerzia data dalla massa. Momento di forza implica accelerazione angolare. E l’inerzia, in questo caso, chi ce la mette? Pensate di mettere in moto rotazionale, agendo con un momento di forza, una giostra senza bambini a bordo e poi la stessa carica di bambini felici. Ovviamente si fa più fatica (ci vuole più momento di forza) nel secondo caso perché c’è più massa da mettere in moto. Ma c’è un’altra cosa da osservare: pensate ora di confrontare la stessa giostra, stessi bambini, però collocati in un primo caso molto vicini al centro della giostra, in un secondo sul suo bordo esterno. Di nuovo, provare per credere: si fa più fatica, a parità di spinta, nel secondo caso. Questo perché i bambini, allontanandosi dal centro, hanno aumentato – senza cambiare la massa della giostra – quello che si chiama “momento di inerzia” del sistema. Una specie di misura pesata della massa e della sua distanza dall’asse di rotazione. La legge di moto di Newton per la rotazione dunque prevede che un momento di forza generi un’accelerazione angolare direttamente proporzionale a esso: la costante di proporzionalità essendo in questo caso il momento d’inerzia, ovvero le masse e il loro “sparpagliamento” dall’asse di rotazione. Domanda finale: vi siete chiesti come mai le ruote delle automobili non sono piene di gomma ma di aria? Dovrebbe essere molto più difficile incappare in una foratura, eppure…