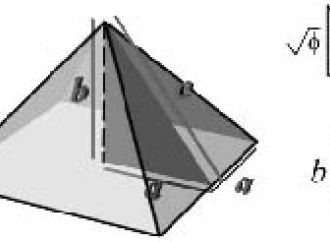
"Quindi", esitò Belbo, "questo signore sta dicendo semplicemente delle verità assodate".
"Verità?" rise Agliè, […] "Quid est veritas, come diceva un mio conoscente di tanti anni fa. In parte si tratta di un cumulo di sciocchezze. Per cominciare, se si divide la base esatta della piramide per il doppio esatto dell'altezza, calcolando anche i decimali, non si ha il numero bensì 3,1417254. Piccola differenza, ma conta. Inoltre un discepolo del Piazzi Smyth, Flinders Petrie, che fu anche il misuratore di Stonehenge, dice di aver sorpreso il maestro che un giorno, per far tornare i conti, limava le sporgenze granitiche dell'anticamera reale... Pettegolezzi, forse, ma il Piazzi Smyth non era uomo da ispirare fiducia, bastava vedere come si annodava la cravatta. Tuttavia fra tante sciocchezze ci sono anche inoppugnabili verità. Signori, vogliono seguirmi alla finestra?"
Spalancò teatralmente i battenti, ci invitò ad affacciarci, e ci mostrò lontano, all'angolo fra la stradetta e i viali, un chioschetto di legno, dove si vendevano presumibilmente i biglietti della lotteria di Merano.
"Signori", disse, "invito loro ad andare a misurare quel chiosco. Vedranno che la lunghezza del ripiano è di 149 centimetri, vale a dire un centomiliardesimo della distanza Terra-Sole. L'altezza posteriore divisa per la larghezza della finestra fa 176/56 = 3,14. L'altezza anteriore è di 19 decimetri e cioè pari al numero di anni del ciclo lunare greco. La somma delle altezze dei due spigoli anteriori e dei due spigoli posteriori fa 190 x 2 + 176 x 2 =732, che è la data della vittoria di Poitiers. Lo spessore del ripiano è di 3,10 centimetri e la larghezza della cornice della finestra di 8,8 centimetri. Sostituendo ai numeri interi la corrispondente lettera alfabetica avremo C10 H8, che è la formula della naftalina".
Tratto da Umberto Eco (1988), Il pendolo di Foucault, Milano: Bompiani, capitolo XLVIII.