La maggior parte delle persone è convinta che termini come Sezione aurea o Proporzione aurea siano antichissimi, risalendo addirittura ai primordi degli studi matematici. In realtà ci troviamo davanti ad un prodotto del XIX secolo.
A ben vedere l’Ottocento ci ha regalato una straordinaria quantità di “leggende”, tra l’altro molto difficili da smascherare perché spesso diffuse come verità scientifiche. Se n’è accorto anche Eugenio Battisti, che all’interno della sua biografia dedicata al Brunelleschi scrive: “L’Ottocento, inoltre, schematizza e rettifica il Brunelleschi nel momento in cui lo misura e lo documenta, semplificandolo proporzionalmente, e dando così adito alle più bizzarre interpretazioni, tipo proporzione aurea”^[1].
Negli stessi anni esplose quella che oggi chiameremmo una sorta di “egittomania” o meglio ancora di “classicomania”. Mentre i piedi dei tavolini venivano foggiati a mo’ di colonne, e le donne della borghesia riscoprivano le acconciature romane, qualcuno inventava nuovi ed esotici nomi per quel rapporto matematico che gli antichi greci chiamavano semplicemente sezione o al massimo “divisione in media ed estrema ragione”^[2]. D’altronde tra breve vedremo come anche la credenza secondo cui le piramidi conterrebbero intenzionalmente sia phi che π abbia inizio da una pubblicazione dell’Ottocento.
Ma procediamo per ordine. In antichità esisteva l’espressione “il giusto mezzo” o più raramente “la media d’oro” solo per indicare l’annullamento degli eccessi di due direzioni opposte; qualcosa tipo il detto “la virtù sta nel mezzo”, che non aveva nessun legame con la famosa proporzione. Una prima trasformazione del termine originale, unita anche a molte aggiunte riguardanti le proprietà estetiche di phi avverrà quasi un millennio e mezzo più tardi, ad opera di Luca Pacioli, che gli dedica la sua opera più famosa, il De Divina Proporzione. Keplero un centinaio di anni dopo riprese il discorso scrivendo: “La geometria ha due grandi tesori: uno è il teorema di Pitagora; l’altro, la divisione in media ed estrema ragione. Possiamo paragonare il primo ad una misura d’oro, e chiamare il secondo un prezioso gioiello”.
Qui l’oro va al teorema di Pitagora, mentre phi si accontenta solo dell’argento. La denominazione attuale invece arriverà ancora più tardi, nel XIX secolo. D. H. Fowler ci riferisce^[3] che il termine sezione aurea, o più precisamente Goldener Schnitt lo troviamo per la prima volta nel 1835, all’interno del lavoro Die reine Elementar-Mathematik di Martin Ohm, fratello del più celebre Georg Simon Ohm, il fisico che ha dato il nome alla misura delle resistenze elettriche^[4]. Più influente nell’introduzione del nuovo termine fu la pubblicazione da parte di A. Wiegang, del saggio Der allgemeine goldener Schnitt und sein Zusammenhang mit der harmonischen Teilung, del 1849.
Infine l’uso di phi per rappresentare il numero aureo fu introdotto in tempi relativamente recenti dal matematico Mark Barr. La conoscenza della vera età del termine, oltre a disincantarci rispetto alle sue antiche origini, ci offre anche un altro importante spunto di riflessione: furono gli studiosi del XIX secolo ad usare l’aggettivo “aurea”, mentre per i greci era semplicemente un particolare metodo di divisione geometrica in media ed estrema regione.
E se per gli antichi non fosse stata tanto più importante di altre costruzioni euclidee? Vedremo ora come la presenza dei due famosi numeri possa essere semplicemente una conseguenza non voluta dell’utilizzo di particolari tecniche di misurazione.
Le piramidi contengono π e Φ per puro caso
Gran parte del fascino esercitato da phi è dovuto alle antiche origini che gli vengono attribuite. Qualcuno cita addirittura uno dei più antichi testi egiziani giunti fino a noi, quello noto come papiro Rhind^[5], che ad un certo punto parla della sacra proporzione utilizzata nella costruzione delle piramidi, anche se non dice affatto quale sia questa proporzione. Tuttavia sembra che Erodoto^[6] riferisca di un particolare accorgimento dettato dai sacerdoti egiziani, che volevano l’area di ogni faccia triangolare pari a quella del quadrato avente per lato l’altezza della piramide stessa, misurata a piombo dall’apice del monumento sino al terreno.
Il matematico Herbert Westren Turnbull^[7] dedica una parte della sua attenzione a tale descrizione all’interno del suo The Great Mathematicians, edito intorno agli anni Cinquanta del XX secolo: “C’è un brano oscuro in Erodoto che può, attraverso una lieve licenza letteraria, essere interpretato in modo da produrre un senso molto chiaro. Esso implicherebbe che l’area di ognuna delle facce triangolari della Piramide sarebbe uguale al quadrato della sua altezza verticale, e questo in effetti è in accordo con la realtà. Se così fosse, il rapporto tra altezza, inclinazione e base potrebbe essere espresso in termini di Sezione Aurea tra il raggio di un cerchio e il lato del decagono inscritto. In breve, esisteva già una conoscenza geometrica ed aritmetica di cui i sacerdoti dell’Antico Egitto avevano fatto tesoro, ben prima che i viaggiatori greci acquistassero le loro conoscenze matematiche”^[8].
Analogamente anche altri studiosi, come Martin Gardner^[9] e David Burton riconoscono le stesse prescrizioni: “Erodoto scrisse in un brano che un sacerdote egiziano gli disse che le dimensioni della Grande Piramide erano state scelte in quel modo affinché l’area di un quadrato la cui altezza era pari a quella della Grande Piramide fosse uguale all’area della sua faccia triangolare”^[10].
In effetti bisogna riconoscere che rispettando questa regola, otteniamo un’altra famosa figura geometrica, il triangolo aureo^[11].
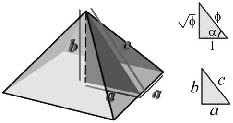
Infatti, l’area di ogni faccia triangolare si ottiene con la nota formula (*):



poiché l’ipotenusa c del triangolo in sezione costituisce l’altezza della faccia della piramide. L’equazione imposta dai sacerdoti sarebbe dunque



dove b è l’altezza della piramide.

Applicando sempre al triangolo abc anche il teorema di Pitagora, esprimendolo però in funzione di b², stabiliremo anche la relazione b² = c² - a², che sostituita nella (*) fornisce





Da qui otteniamo i due valori di c:



Trascurando il valore negativo, possiamo calcolare il rapporto che deve esistere tra c ed a:



In base alla (*) ricaviamo anche b, per cui assegnata la misura a del semilato della base della piramide, le altre dimensioni si calcolavano di conseguenza (§):



Ponendo a = 1 si ottiene il triangolo aureo, di lati



Non è chiaro il motivo che avrebbe spinto i sacerdoti egiziani a cercare queste proporzioni, tuttavia bisogna osservare che il triangolo aureo di base 1 semplifica notevolmente molti calcoli trigonometrici, ammesso che gli egiziani avessero un qualche metodo per utilizzare agevolmente phi e soprattutto la sua radice^[12]. Infatti:



L’angolo alfa è dunque di 51° 49’ 38” 252.

Non è possibile prescindere da straordinarie corrispondenze, ad esempio con la piramide di Cheope, le cui misure sono riportate anche nel primo volume della Storia della Scienza, dell’Enciclopedia Italiana Treccani: “La tecnica della piramide di blocchi di pietra raggiunse il suo apogeo nel corso del regno di Cheope (2600 ca.), figlio di Snofru, il quale scelse la pianura di Giza per la costruzione del suo complesso piramidale.
Nacque così la Grande piramide, le cui proporzioni rasentano il rapporto di equilibrio ideale. All’origine il monumento misurava 230 m. ca. di lato di base per 147 m. ca. di altezza, con facce inclinate di ca. 51°50”.
In base a questi dati è facile fare qualche semplice calcolo: a = 230/2 = 115 m.; b = 147 m. Grazie al teorema di Pitagora otteniamo c² = 13225 + 21609, ovvero c = 186,64 m. A questo punto possiamo verificare il rapporto c/a: 186,64 : 115 = 1,6229 che come si vede è vicinissimo a phi.
D’altronde l’area della faccia triangolare risulta essere di 21463,6 m², molto prossima a quella del quadrato dell’altezza, pari a 21609 m². E poi è sin troppo semplice notare che le due inclinazioni praticamente corrispondono.

Seguendo le indicazioni dei sacerdoti egiziani si ottiene anche un altro effetto, che ha scatenato spesso straordinarie speculazioni esoteriche. Infatti esiste anche una relazione approssimata tra phi e pi greco:



Il reale valore di pi greco è 3,1415... mentre questa formula fornisce un risultato di 3,1446..
Nei pochi passaggi che stiamo per fare chiameremo questo numero π_a. Le conseguenze pratiche di ciò sono molto importanti; tornando alla prima formula della (§), avremo



Continuando ci accorgiamo che



ma 8a non è altro che il perimetro della base della piramide, per cui questa possiede:
“La proprietà geometrica unica che la sua altezza sta nello stesso rapporto al suo perimetro, come il raggio rispetto alla circonferenza di un cerchio”^[13]. E questo molti secoli prima che i greci fornissero la definizione rigorosa di pi greco.
Nonostante tutta questa apparente sapienza matematica ci sono dei validi motivi per non credere che gli egiziani conoscessero realmente tali numeri. A partire dal testo di Erodoto che non è affatto chiaro, per cui può dare luogo a diverse interpretazioni. Quelle di Turnbull, Gardner e Burton non sono assolutamente condivise da altri studiosi, tra i quali spiccano Richard Gillings^[14], Roger Fischler^[15] e George Markowsky^[16]. Tutti e tre dichiarano che Erodoto fornisce semplicemente le dimensioni della piramide e non parla assolutamente di eguaglianza tra aree.
Fischler ha rintracciato l’origine dell’interpretazione “esoterica” accorgendosi che, come al solito, essa risale all’ottocento, e precisamente compare per la prima volta nel libro del piramidologo John Taylor, The Great Pyramid, Why Was It Built and Who Built It?, pubblicato nel 1859.

Inoltre, se andiamo a leggere una traduzione molto attendibile, e vicinissima a quella letterale, ad esempio delle edizioni U.T.E.T., ci accorgiamo che occorre davvero un notevole sforzo di fantasia per trovare dei riferimenti ad aree e non a semplici misure lineari: “Per erigere la piramide stessa furono invece necessari venti anni di tempo; è quadrata e ogni faccia ha la base di otto plettri e un’uguale altezza; è formata da blocchi di pietra levigati e perfettamente connessi; nessun blocco misura meno di trenta piedi”^[17].
Il plettro è un’antica unità di misura, pari a 100 piedi, ossia a 30 m. circa. Quindi le dimensioni che Erodoto riferisce riguardo i lati sono abbastanza precise, essendo circa 240 m. contro i 230 misurati oggi. Un’altezza di otto plettri è invece totalmente errata, risultando quasi il doppio di quella reale. Nonostante questo possa alimentare qualche dubbio, la teoria dell’equivalenza delle aree sembra più una coincidenza adattata con criteri postumi che un qualcosa di voluto.
Comunque, prescrizione dei sacerdoti o meno, vi sono almeno due ipotesi sensate che spiegano la geometria della piramide, e dimostrano che non era assolutamente necessaria una conoscenza della sezione aurea o del famoso pi greco. Una è riportata nel libro di Gillins^[18], e riguarda la necessità di mantenere costante una determinata pendenza, mentre l’altra, molto attendibile ed esauriente, viene spiegata in modo chiaro nell’interessante libro di Kurt Mendelssohn^[19], ed è stata pensata da un ingegnere elettronico, T.E. Connolly^[20]. Si basa su di un concetto fondamentalmente semplice, per cui gli egiziani avrebbero usato due unità di misura, una per le piante ed una per gli alzati. Infatti le corde in fibra di palma si sarebbero rivelate troppo imprecise per le lunghe distanze, inducendoli ad usare una grande ruota, di diamentro ben definito, una specie di odometron^[21]. È come se noi facessimo un ragionamento di questo tipo: prendo una ruota di 1 m di diametro e poi faccio un edificio largo 10 giri e alto 10 m. Ovviamente otterrò una costruzione le cui dimensioni sono tra loro in rapporto di pi greco.
Secondo questa teoria gli egiziani avrebbero usato il semplicissimo rapporto^[22] di 1:4, con calcoli del tipo “prendo una ruota del diametro di 1 cubito, faccio 200 ‘cubiti girati’ di larghezza e 800 cubiti di altezza”^[23].
Così il triangolo in sezione avrebbe avuto una base lunga nπ ed un’altezza di 4n. In tal modo il perimetro della piramide sarebbe stato i 8nπ, per cui il suo rapporto con l’altezza avrebbe restituito il famoso 2π.
Inoltre per il teorema di Pitagora l’ipotenusa sarebbe stata quindi pari a



per cui tutto ciò avrebbe portato casualmente gli egiziani non solo ad utilizzare precocemente pi greco nei loro edifici, ma anche, con buona approssimazione il celebre numero d’oro:



Questa teoria è molto credibile, perché spiega perfettamente anche l’inclinazione delle poche piramidi di 43°. E poi è molto più sensato pensare che i sacerdoti avessero individuato il rapporto di 1:4 piuttosto che fossero in grado di dominare numeri irrazionali e trascendenti.
Con un po’ di impegno, tutto è basato su Φ
È ovvio che è sin troppo facile giocare con i numeri. Gran parte delle ‘scoperte’ riguardanti le proporzioni sono basate su dimostrazioni di destrezza aritmetica. Così, senza nessun criterio teorico viene scelto uno spigolo tra i dieci di una modanatura, e viene messo in relazione magari con un quinto della lunghezza della terza finestra a sinistra...
Lavorando in questo modo è possibile individuare rapporti proporzionali praticamente ovunque, anche perché, per un calcolo probabilistico, all’interno di un qualsiasi scarabocchio composto già solo da qualche decina di linee spezzate si trovano praticamente tutti i rapporti che desideriamo, anche con una tolleranza molto precisa.
Tutto sta nello scegliere i punti giusti per sostenere i vari ragionamenti.
Questo non significa che nell’architettura non esistano proporzionamenti modulari, ma sicuramente suggerisce che occorre molta attenzione e professionalità per affrontare uno studio del genere. Uno degli articoli più critici e fondati realizzato negli ultimi tempi è stato quello pubblicato da Livio Volpi Ghirardini^[24] e Marco Frascari^[25] in occasione del NEXUS’98^[26] dal significativo titolo Contra Divinam Proportionem. Qui la sezione aurea viene descritta come una “aurea o divina lente di ingrandimento che distorce tutte le regole realmente applicate all’architettura, in nome dell’estetica e di impulsi mistici”.
Per i due autori la ricerca della sezione aurea è stata portata avanti da una sorta di fanatici – che essi ironicamente chiamano Φ – edeli – che ignorando la realtà dell’architettura e le regole di costruzione hanno voluto per forza ritrovare phi in ogni antica costruzione. La loro critica inizia dai fondatori moderni della teoria, Zeising e Gunter, che per provare la presenza della gold section ricorsero a degli schemi tracciati su delle foto. A tal proposito Frascari e Ghirardini dicono che: “Senza alcun dubbio Zeising e Gunter sono molto abili a misurare le fotografie, ma è chiaro che nessuno di loro ha mai misurato un edificio”.
Infatti, come ben sanno i tecnici, il problema dell’errore di misurazione è molto importante, e spesso viene manipolato a proprio piacere dai ricercatori troppo teorici. Così, se consideriamo un margine dell’uno per cento al momento del rilievo di due grandezze A e B, il rapporto A/B che ne deriverà avrà una tolleranza del 2%:



Questo permetterebbe di accettare come sezione aurea valori che oscillano tra 0,59 e 0,63, includendo quindi una vastissima rosa di rapporti.
Frascari e Ghirardini riportano alcuni esempi documentati dell’uso da parte di architetti di proporzioni quali 5/3 e 8/5, facendo notare come questi si avvicinino a phi, soprattutto considerando il discorso sulle tolleranze. Analogo ragionamento viene fatto da Pierre von Meiss^[27], quando dice che “il rapporto aureo è molto vicino al rapporto di 5/8”.
Questa libertà matematica, unita all’arbitrarietà con cui vengono scelti i riferimenti, rende veramente molto semplice trovare phi in qualunque edificio. Sempre i due già citati autori giungono a dire che “per i credenti di phi, ogni punto è buono per posizionare il punto”. E qui gli edifici rischiano di comportarsi come il buon vecchio Hans.
Certo, la sezione aurea, in quanto conseguenza di molte costruzioni geometriche di base, è stata utilizzata dagli antichi, più o meno coscientemente. Si ritrova infatti in alcuni triangoli rettangoli ed isosceli, nel pentagono, nel decagono, nella stella di David ed in alcune spirali per cui in un modo o nell’altro esce sempre fuori...
Paul-Alan Johnson, nel suo recente libro The Theory of Architecture: Concepts, Themes and Practices, condivide la teoria di costruzioni geometricamente basilari - per la maggior parte empiriche - come unica base per i tecnici di duemila anni di architettura. Egli scrive che, nel corso della storia, molti architetti hanno posseduto unicamente “una conoscenza rudimentale della geometria e della progettazione, utilizzando permutazioni più o meno dirette di poligoni regolari e cerchi. Con il rischio di semplificare un po’ troppo, si può dire che per più di due millenni basiliche, duomi e strutture a volta sono state disegnate principalmente da proiezioni o rotazioni di tre figure primarie - cerchio, rettangolo e triangolo”^[28].
Ovviamente questo non significa che le planimetrie e gli alzati fossero semplici, anzi, forse il segreto degli antichi stava proprio nel saper fare grandi realizzazioni architettoniche e tecnologiche utilizzando strumenti e regole molto semplici, alcune delle quali veramente perdute^[29].
Sempre all’interno del Nexus le idee di Gherardini e Frascari vengono appoggiate anche da un altro storico, Rocco Leonardi, che evidenzia come qualsiasi dilettante della geometria o anche un semplice studente possa accidentalmente costruire delle figure contenenti casualmente la sezione aurea.


D’altronde questo punto di vista non è nuovo, come dimostrano le parole dell’eminente storico della matematica Georges Ifrah: “Conoscevo una volta un professore di matematica che [...] voleva convincere i suoi studenti che la geometria astratta precedeva storicamente le sue applicazioni pratiche, e che le piramidi e le costruzioni dell’antico Egitto “dimostravano” che i loro architetti erano matematici altamente sofisticati.
Ma il primo giardiniere della storia che ottenne una perfetta ellisse con tre pioli e una corda certamente non aveva alcuna conoscenza di teoria delle coniche! Né gli architetti egiziani avevano altro se non semplici strumenti - ‘trucchi’, ‘sotterfugi’ e metodi di tipo totalmente empirico, senza dubbio scoperti nel corso di svariati tentativi - per realizzare i loro progetti. Sapevano, ad esempio, che se si prendono tre pezzi di corda che misurano rispettivamente tre, quattro e cinque unità di lunghezza, e li si collega tra loro, se si fissa l’anello a terra con un piolo ad ogni nodo, si ottiene un perfetto angolo retto. Questo ‘trucco’ dimostra il teorema di Pitagora [...] ma non presuppone la conoscenza di formule astratte, che quasi certamente gli egizi non avevano”^[30].
Opinione, questa, che si ricollega perfettamente a quanto detto riguardo l’utilizzo da parte degli egiziani di un rullo graduato per la costruzione delle piramidi.
Abbiamo diversi altri esempi riguardanti l’uso involontario della matematica superiore. Sempre all’interno del Nexus Journal, Paul Calter nel suo interessantissimo articolo intitolato “How to Construct a Logarithmic Rosette (Without Even Knowing it)”, dopo aver riportato un paio di noti esempi di rosette realizzate in età classica e medioevale^[31], dimostra matematicamente che le curve costruite appartengono alla spirale logaritmica. Ovviamente gli scultori non conoscevano i logaritmi, ma questi vengono ottenuti involontariamente con una semplice costruzione ripetuta.
Ma allora i grandi architetti del passato hanno creato straordinarie strutture archimatematiche per puro caso? No, perlomeno non in tutti i casi. Ma bisogna pensare alla costruzione del rapporto aureo come una delle tante insegnate dalla dottrina geometrica, e non come il retaggio di un’antica e misteriosa sapienza che ha forgiato tutti i principali monumenti della storia. Come il sacro taglio dei romani o la vesica pisces, la sezione aurea veniva indubbiamente utilizzata nell’antichità, ma con molta probabilità il suo uso derivava da una pratica empirica, ben lungi dalla profonda conoscenza matematica e simbolico-filosofica che si vuol per forza dare ai suoi utilizzatori. E spesso è presente anche laddove non era stata pensata, perchè implicita in diverse figure elementari.
In realtà, forse l’unico monumento sul quale non abbiamo problemi di misurazioni ed attribuzioni è il Teatro di Epidauro, che contiene dei riferimenti discreti: i 55 gradini divisi in due parti, una di 34 e l’altra di 21, che si trovano tra loro in un rapporto vicinissimo a phi. Per altri casi, incluso il celebre Partenone, i punti sono scelti arbitrariamente, ad esempio ritrovando phi nel rapporto tra larghezza (considerando anche quello dei gradini dello stilobate) e altezza (misurandola solo sin dove arriva il triangolo interno, che doveva ospitare le sculture, ed evitando lo spessore del tetto...).
Lo stesso dicasi anche per phi che viene “ritrovato” anche in molte opere d’arte, vasi, sculture e cosi via... Prendiamo per esempio il San Girolamo di Leonardo, che si vuole inscritto in un rettangolo aureo. Osservando la fig.3 viene spontaneo chiedersi per quale motivo un esteta ricercatore dell’equilibrio avrebbe deciso di amputare in malomodo il braccio del santo, ritenendo (chissà per quale motivo) che esso non dovesse far parte della composizione: un’inutile appendice protuberante senza nessuna importanza visiva, tanto da non essere incluso all’interno della sacra proporzione.
L’uso della sezione aurea, ampiamente diffuso durante il Rinascimento, subì un duro colpo durante il XVII secolo, quando l’avvento del positivismo lo criticò duramente, relegandolo tra le superstizioni popolari.
Da un lato tale atteggiamento eclissò la teoria per quasi due secoli, ma dall’altro fu preparatorio per un nuovo approccio, di tipo scientifico, che si sarebbe imposto non prima del XIX secolo. Se all’inizio tale verifica sembrava (doveva?) dare per forza risultati incoraggianti riguardo la valenza estetica di phi, con il perfezionarsi dei metodi di indagine le prove di questa supposizione sono divenute via via sempre più vaghe, sino ad un’inversione di tendenza.
Oggi i maggiori ricercatori considerano le proprietà estetiche della sezione aurea come una fantasia al pari degli antichi miti.

Pubblicato su "Indagini su Rennes-le-Chateau",
si ringrazia l'editore per aver concesso il diritto di riproduzione

Note