La ricerca ci piace, la spiegazione delle maree no
Tuttavia mi sento in dovere di fare una critica alla spiegazione gravitazionale delle maree fornita nell'articolo, perché a me sembra di averla capita in un altro modo. L'assenza di maree in una vasca da bagno non è dovuta alla piccola massa dell'acqua contenuta, perché è vero che l'attrazione lunare è direttamente proporzionale anche a questa massa, ma la conseguente accelerazione è inversamente proporzionale alla stessa massa e allora pari e patta: l'oceano Pacifico e la vasca da bagno sono paritetici. Il fatto è che gli effetti mareali dipendono dal gradiente della forza di attrazione, cioè vanno come r alla meno tre: la marea non è un "sollevamento", ma una "deformazione" e la vasca da bagno non si deforma perché è piccola, mentre l'oceano Pacifico si deforma perché è grande e la forza di attrazione lunare non è uguale in tutti i suoi punti. Tra l'altro mi sembrerebbe proprio necessario precisare che quando c'è qui, l'alta marea c'è anche agli antipodi. È come dire che il davanti e il didietro della Terra sono in caduta libera verso la Luna (come la Luna lo è verso la Terra), ma con velocità diverse, essendo a diverse distanze da questa e allora il geoide si deforma diventando come un pallone da rugby: l'argomento dell'alta marea agli antipodi non consente troppe semplificazioni alla teoria delle maree.Insomma, mi sentirei di affermare che su un ipotetico pianeta puntiforme di massa grande a piacere (ma deformabile) e immerso in un campo gravitazionale grande a piacere, non ci sarebbe nessun effetto mareale, perché non ci sarebbe nessun gradiente di questo campo che potrebbe deformarlo.
Adalberto Piazzoli,
Past President CICAP
Risponde Alessandra Ventrice
Insieme alla lettera di Piazzoli ne abbiamo ricevuta un'altra sullo stesso tema di Lodovico Marchetti, illusionista ed ex direttore dell'osservatorio astronomico del Comune di Pietrasanta. Ad entrambi voglio dire che le non solo sono assolutamente corrette, ma doverose. Vi ringrazio per aver apprezzato il resto del lavoro e per aver capito quale fosse l’obiettivo didattico di tale analisi. Purtroppo per me mi sono imbattuta in un argomento tutt’altro che semplice e che nasconde un “mare” di insidie.
Per spiegarlo in modo che gli alunni capissero, non potevo certo parlare di rapporto differenziale. Ciò non toglie che le mie conclusioni, estrapolate per altro da libri di testo in uso nelle scuole, hanno portato ad una conclusione sbagliata. Il mio è stato un tentativo un po’ azzardato di spiegare a dei ragazzi che la frase, “come la Luna influenza le maree allo stesso modo può influenzare le nascite”, non ha senso, perché fasi lunari e attrazione gravitazionale sono due fenomeni diversi. La pubblicazione del lavoro sulla rivista voleva dimostrare che all’interno della scuola si possono condurre piccole indagini, dove non è tanto importante il risultato ottenuto, quanto il metodo, il percorso che è stato intrapreso per ottenere tale risultato, se poi questo è significativo tanto meglio!
Le vostre lettere sono state per me spunto di riflessione, ed è proprio per questo che mi sono già attivata per cercare nuovi materiali per spiegare ai ragazzi in modo semplice, ma corretto, il complesso funzionamento delle maree.
Sappiamo valutare le inclinazioni?
Ho letto con interesse l'articolo sull' illusione dell'elevazione di Stefano Vezzani (Query 19) e mi chiedevo se la difficoltà della misurazione “ad occhio” dell'elevazione non sia in qualche modo legata alla difficoltà di valutare correttamente le inclinazioni in generale.
Se mediamente nelle valutazioni dell'elevazione verso l'alto ci si sbaglia con errori fino a 20° è anche vero che ci si sbaglia quasi altrettanto nel valutare le inclinazioni verso il basso.
È abbastanza normale che nel giudicare un prato piuttosto ripido o un pendio innevato, o anche la falda di un tetto, lo si consideri sempre più inclinato, più ripido di quanto non sia in realtà, anche se non si tratta di “cielo percepito”.
Considerando i pendii innevati ad esempio (abito in montagna), è tanto più facile cadere in errore quanto più il pendio è privo di punti di riferimento. I vasti pendii detritici o prativi estivi, quando innevati ed osservati dall'alto, sembrano molto più ripidi di quello che sono, pur considerando l'estrema variabilità soggettiva del giudizio di ripido. Non solo.
Se disegnamo un angolo di 30° o 40° sulla carta, senza quantificarlo numericamente, e ci immaginiamo di essere sulla cima di un pendio con quella inclinazione, quasi nessuno, osservando il disegno, lo considera ripido.
Il pendio appare elementare ed affrontabile anche con attrezzatura banale, addirittura con sci da fondo, per capirci. Ben diversa è invece la situazione quando siamo in cima ad un pendio reale con la stessa inclinazione.
Certo per un pendio da scendere con gli sci subentra il fattore delle capacità tecniche e soprattutto delle condizioni della neve; un manto di neve soffice anche parecchio ripido, a parità di inclinazione, è molto più facile di un pendio di neve trasformata e ghiacciata dove il più piccolo errore potrebbe essere l'ultimo!
Resta comunque il fatto che quando si giudica la pendenza, ovvero l'inclinazione, la maggior parte delle persone, anche scialpinisti esperti, sono propense a sopravvalutarne, numericamente, la ripidità.
L'errore medio è un po' inferiore dell'errore di valutazione dell'elevazione. Diciamo che mediamente è di 10° ma arriva anche ai 15°, in buona fede, tra chi ha meno esperienza e magari anche meno tecnica.
Ovvio che l'esercizio di valutazione, aiutandosi magari con uno strumento anche semplicissimo come un “inclinometro” casalingo, porta ad affinare l'occhio fino a sbagliare di molto poco la misura, ma questo vale per tutte le cose. Passare dalla valutazione qualitativa ed estremamente soggettiva ad una valutazione quantitativa è possibile solo con l'esercizio.
In effetti, l'errore di giudizio circa l'elevazione/pendenza non implica che noi non siamo in grado di valutare se un pendio - che sia un prato, una falda di un tetto, rocce o neve - sia ripido o meno.
Il nostro istinto di sopravvivenza ce lo fa considerare ripido ove il concetto di ripido è però estremamente elastico e soggettivo.
Quello che evidentemente non siamo in grado di fare, se non con la pratica, è quantificarne numericamente la ripidità, ovvero l'inclinazione, con ragionevole precisione. Del resto l'esprimere il concetto di pendenza in “gradi” è sicuramente un costrutto culturale e non innato.
Si potrebbe dire che l'evoluzione ci ha fornito i mezzi per valutare la ripidezza, in salita o in discesa, fino appunto a pendenze intorno ai 30° / 40° che sono ragionevolmente gestibili, salibili o scendibili, senza eccessivi pericoli.
Oltre c'era forse l'inaccessibile o l'indiscendibile, in ogni caso qualcosa di scarso interesse.
Non so se alla base degli errori di valutazione dell'elevazione e della pendenza ci possa essere lo stesso meccanismo psicologico ma mi incuriosisce la somiglianza dell' osservazione.
Gabriele Scanavino
Entracque
Risponde Stefano Vezzani
Le sue osservazioni sono ampiamente confermate da diversi lavori sperimentali: se le si guarda frontalmente, sia le salite che le discese sembrano molto più ripide di quanto in realtà non siano.
Mi chiede se alla base dell’illusione dell’elevazione e della sovrastima delle pendenze non ci possa essere lo stesso meccanismo.
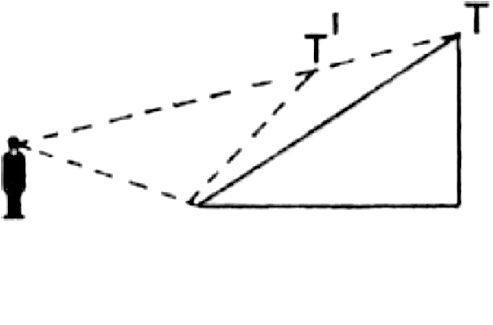
Credo non lo si possa escludere, ma, a quanto mi risulta, una spiegazione comune convincente non è stata ancora proposta da nessuno. Tra quelle che conosco, l’unica spiegazione che può essere applicata sia alla sovrastima delle salite (ma non delle discese) che all’illusione dell’elevazione è quella relativa alla percezione delle distanze che von Sterneck ha formulato nei primi anni del secolo scorso. Essa è messa in crisi, però, tra le altre cose proprio da alcuni dei fenomeni che lei descrive e di cui diversi esperimenti confermano l’esistenza, come spiegherò tra poco.
Figura 1
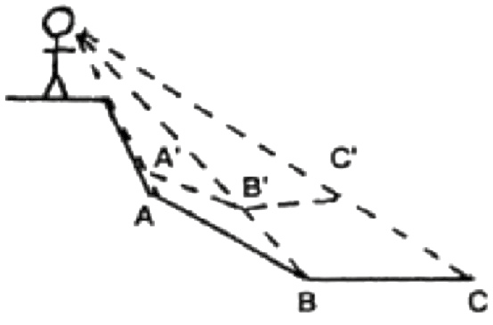
Ma la teoria di von Sterneck prevede anche che le discese sembrino meno ripide del vero, come si può vedere nella figura 2: la discesa reale è ABC, mentre quella percepita dovrebbe essere, secondo von Sterneck, A’B’C’. In realtà, proprio come nota lei, succede il contrario, perché anche le discese sono molto sovrastimate, almeno quanto le salite. Ad esempio, nel 1967 Kammann trovò che una discesa di 34° era stimata di circa 50° e Ross (2010) ha trovato di recente che una discesa di 7° viene giudicata di 23° se la si osserva dall’orlo.
Figura 2
Alla teoria di von Sterneck sono state mosse anche altre obiezioni, di cui però non è il caso di parlare qui.
Per una descrizione più dettagliata della teoria di von Sterneck e per il modo in cui essa può spiegare l'illusione dell'elevazione rinvio a Minnaert (1993). I testi che ho citato, incluso quello di Minnaert, sono scaricabili da qui: http://tinyurl.com/kqz3yv3 .
