In italiano sono due le parole che esprimono la facoltà o l'atto di vedere: a) vedere appunto e b) guardare.
Il senso etimologico di questi due verbi è "avere imparato da" (vedere < weid, termine indoeuropeo) e "stare attento a" (guardare < weg, termine indoeuropeo). Ciò ci indica che per i nostri lontani antenati un'immagine è qualcosa da cui si trae un'informazione (ho imparato da) o da seguire con attenzione (sto attento a).
Sfortunatamente (o fortunatamente?) la visione non è percezione diretta della realtà. Infatti, il nostro cervello analizza, filtra e interpreta ogni stimolo che viene riportato sulla retina. Se così non fosse, probabilmente non saremmo tuttora in grado di vedere i colori (i colori sono un'invenzione della mente, il mondo reale è in bianco e nero!) e vedremmo il mondo circostante capovolto. Un altro paradosso interessante della visione è che ai limiti del nostro campo visivo dovremmo scorgere delle zone nere, invece il cervello ignora e cancella semplicemente queste zone di confine della visione con un effetto fadeout (di dissolvenza) graduale.
G.K. Chesterton ha scritto: un paradosso è il mezzo più utile per aprire gli occhi del mondo a una verità negletta... Noi, più modestamente, ci accontenteremo di proporvi in questa nuova rubrica degli esempi di illusioni, paradossi e rompicapi visuali con lo scopo, non solo di fornire un materiale ludico di utilità professionale o scolastica, ma anche di proporre uno sguardo diverso sull'educazione visiva.
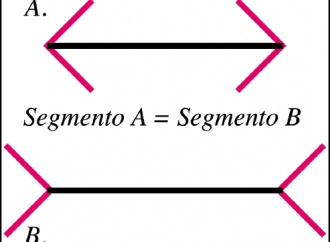
Non bisogna affidarsi ciecamente ai propri occhi... Sono infatti gli organi percettivi più convenzionali che abbiamo! Convenzionali nel senso che interpretano ciò che vediamo (tramite il cervello) secondo schemi prestabiliti. Sapreste indovinare quale freccia, nella figura 1, è la più lunga?
La maggior parte di voi esclamerà: "ma la freccia A, evidentemente!". Ma no... sbagliato! Le due frecce hanno la stessa lunghezza, basta misurare per verificare. Come spiegare questo abbaglio? Perché lo sfondo delle frecce e la loro posizione assoluta creano un contrasto (chiaro/scuro, verticale/orizzontale...) che interferisce con le immagini reali.
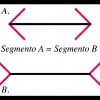
La stessa cosa succede con l'illusione della figura 2. Però, qui, il segmento più lungo è il segmento B (scommettiamo che avete indicato il segmento A...) Questa illusione ottico-geometrica si verifica perché c'è un contrasto di dimensione tra le due ellissi nelle quali sono iscritti i segmenti.
Le cose sembrano diverse nella figura 3, che rappresenta una tavola con specchio, perché i segmenti A e B sembrano davvero uguali... E invece no, il segmento A è più lungo. Anche qui interviene un contrasto, il contrasto di profondità.
Concludiamo con l'illusione della figura 4, nota fin dall'antichità. Il punto B sembra trovarsi a metà distanza tra i due segmenti orizzontali, sembra... perché è il punto C che divide a metà la distanza che separa i segmenti, ci siete cascati ancora una volta, vero?
Gianni A.Sarcone
e Marie J. Waeber
Sono i responsabili e
coordinatori di uno dei migliori siti sul web dedicati ai giochi,
alle illusioni e all'enigmistica: www.archimedes-lab.org