Quest’anno, anche grazie ai membri e agli amici del CICAP, sono salito sul podio con la mia presentazione “Dynamic Müller-Lyer Illusion”, che vi rivelo con piacere in queste pagine.
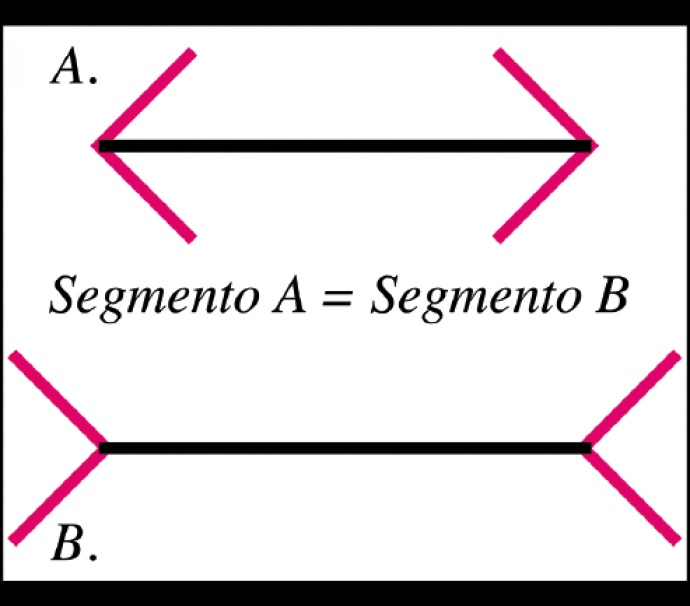
Certo, una linea retta è il percorso più breve tra due punti virtuali. Il contesto può però svolgere un ruolo chiave nell’interpretare la lunghezza di una linea retta. Un segmento può, infatti, apparire più lungo o più corto se racchiuso tra due parentesi angolari, le cui punte sono dirette verso l’esterno (fig. 1.a) o verso l’interno (fig. 1.b). Quest’illusione fu pubblicata dallo psicologo tedesco Franz Carl Müller-Lyer nel 1889 per dimostrare, appunto, la dipendenza di una lunghezza percepita dalle espansioni apicali.
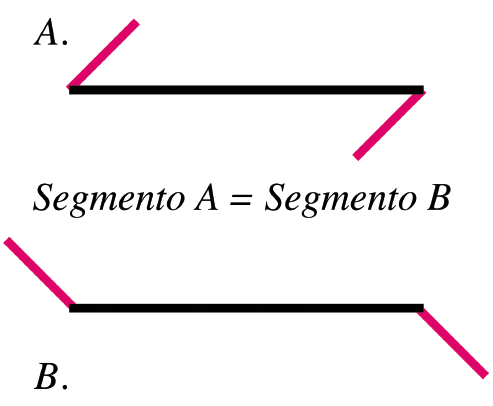
Ora prendiamo una versione adattata da Franz Brentano, un altro psicologo tedesco coevo di Müller-Lyer (fig. 2). Che succede se aggiungiamo del movimento all’illusione, cioè se apriamo o chiudiamo alternativamente le parentesi angolari da più o meno 45 gradi a 135, e viceversa? Il puntino rosso centrale è equidistante dagli altri due puntini rossi, eppure le estremità della linea sembreranno tendenzialmente allungarsi e accorciarsi a turno, come fossero un elastico! Per visionare questo effetto illusorio dovrete ovviamente andare su Youtube[1]. Esiste anche una versione radiale della mia illusione dinamica ancora più spettacolare[2].
Potete sperimentare voi stessi (o sui vostri amici) la potenza di questa illusione. La sfida è la seguente: tracciate un segno sulla lunghezza della fig. 3, detta figura di Judd, con una matita in modo da dividerla in due parti perfettamente uguali. Nel novanta per cento dei casi, la sfida verrà persa.
L’illusione di Müller-Lyer persiste anche con linee curve, come illustrato nella fig. 4, i cui due archi sono del tutto congruenti. Oppure quando vengono spunte le parentesi angolari (fig. 5.a e b).
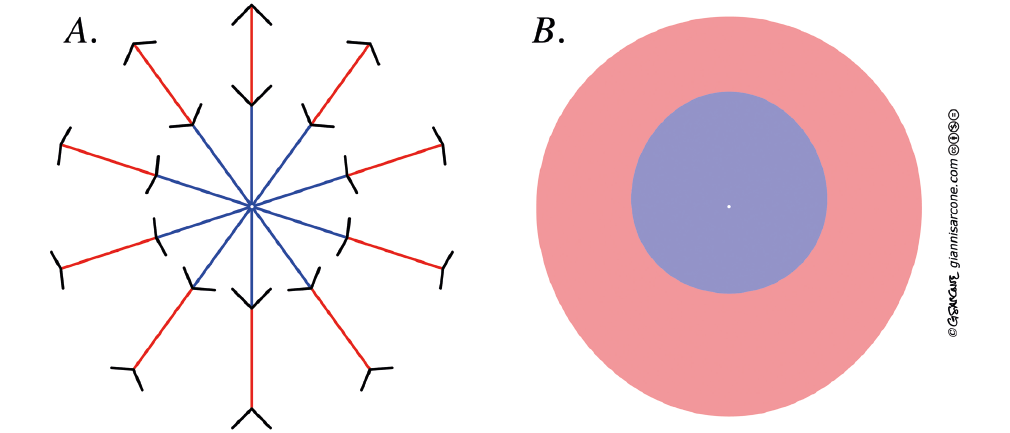
Più sorprendente ancora, l’illusione non è soltanto lineare: coinvolge anche la geometria piana! Nella fig. 6.a, le estremità dei segmenti collineari blu e rossi, disposti radialmente intorno a un punto centrale, delimitano due cerchi perfettamente concentrici. Invece, per la maggior parte degli osservatori, essi delimitano un grande ovoide che circoscrive un altro ovoide, leggermente eccentrico (fig. 6.b). Questo proviene dal fatto che i segmenti rossi sembrano allungarsi verso la parte inferiore della figura, mentre i segmenti blu paiono allungarsi verso la parte superiore della medesima.
Il presunto meccanismo dell’illusione di Müller-Lyer rimane ancora aperto alla discussione. Ma, grazie alla mia illusione dinamica, si può capire che è dovuto più a un fenomeno fisiologico che ad un preconcetto psicologico. Molte illusioni geometriche coinvolgono linee a forma di V. È possibile vedere effetti simili nei tessuti (illusione di Zöllner[3]), nell’illusione lunare (di cui abbiamo parlato su Query 30: la luna appare più grande all’orizzonte in conseguenza dell’illusione di Ponzo[4])), nella distribuzione di una linea in uno spazio chiuso (parallelogramma di Sander[5]), ecc. Un simile effetto illusorio si applica anche alla percezione del tempo: il tempo pieno di attività (linea compatta con le frecce che puntano verso l'esterno) sembra più breve rispetto al tempo vuoto, quando non abbiamo nulla da fare (linea aperta con le frecce che puntano verso l'interno).
Per saperne di più:
- Dal mio sito: http://bit.ly/2jWK0jd
- Dal sito di Scientific American: http://bit.ly/2yCCGOh
Note
Referenze
- Vicario, Giovanni B. Illusioni Ottiche Geometriche, Istituto Veneto di Scienze, Lettere e Arti, p. 25, 2009.
- Müller Illusion, Mathworld: http://bit.ly/2zfcJrD