«I swear to tell the truth, the whole truth, and nothing but the truth, so help me God». La frase, di solito tradotta con «Giuro di dire la verità, tutta la verità, nient’altro che la verità, e che Dio mi aiuti», ce l’hanno insegnata decine di film e telefilm: chi è chiamato a deporre in tribunale negli Stati Uniti deve mettere la mano sulla Bibbia e recitare quella formula di rito. È una formula evocativa e impegnativa, e soprattutto sentita tante di quelle volte che ormai fa parte dell’immaginario collettivo anche per chi non è credente né americano. Sembra comunque che ormai si possa omettere la parte religiosa, ma il resto della narrazione filmica rispecchia abbastanza fedelmente la realtà. Del resto, quel che accade nei tribunali italiani non è poi tanto diverso: il presidente della corte ammonisce i testimoni sull’obbligo di dire la verità e sulle conseguenze a cui si andrebbero incontro se tali obblighi fossero disattesi, e poi, come prescritto dall’articolo 497 del Codice di Procedura Penale, li invita a recitare una formula molto simile: «Consapevole della responsabilità che con il mio esame assumo davanti alla legge, m’impegno a dire tutta la verità e a non nascondere nulla di quanto è a mia conoscenza».

Ma cosa farebbe un matematico, magari proprio un logico, se gli fosse richiesto di pronunciare una simile formula? Ebbene, anche se i matematici (e i logici soprattutto) hanno la fama di puntualizzare e precisare ogni particolare, per la maggior parte sono pur sempre persone normali e come tali hanno paura di finire in galera per oltraggio alla corte; così, con ogni probabilità, metterebbero da parte i dubbi professionali, giurerebbero disciplinatamente e risponderebbero alle domande dei magistrati. Almeno, quasi tutti: è rimasto famoso l’episodio del giuramento di Kurt Gödel per ottenere la cittadinanza americana. Il logico austriaco aveva trovato quella che secondo lui era una falla logica nella Costituzione degli Stati Uniti, e cercò di spiegarla al giudice che presiedeva l’udienza. Per fortuna di Gödel, e con grande sollievo di Albert Einstein e di Oskar Morgenstern che lo avevano accompagnato in aula, il magistrato si limitò a sospirare ed evitò di approfondire l’argomento.

Resta il fatto che quasi certamente i dubbi professionali rimarrebbero anche nelle teste di logici meno rigorosi di Gödel. Ha realmente senso impegnarsi a dire «solo la verità»? Usare una forma di cortesia nei confronti di qualcuno che ci è antipatico, non è già una forma di bugia? Augurare il buongiorno a una persona senza desiderare che abbia una buona giornata, non è un po’ mentire? E che dire di quell’altro impegno maiuscolo, davvero impossibile a mantenersi? Come si può chiedere a un essere umano di dire «tutta la verità»?

Anche scendendo a patti con il buon senso e tacitando il furor logico — e quindi acconsentendo all’idea che la formula del giuramento sottintenda «la verità relativa ai fatti in discussione» — come si può pretendere di trasformare in parole tutte le informazioni ottiche, uditive, tattili, olfattive, di un qualsiasi evento di cui si è stati testimoni? Quale sarà la percentuale di dati che l’umana debole memoria ha registrato in quel marasma di informazioni? E quanti saranno gli errori involontari, di interpretazione o di perdita dei dati elaborati in quel momento cruciale che si chiede di raccontare (sotto giuramento!) con il misero ausilio della sola voce?

Sorvolando sulla terza imposizione del giuramento statunitense («nient’altro che la verità») perché talmente impositivo e pretenzioso da non meritare commenti, forse è bene smetterla con le pignolerie logiche, tornare con i piedi sul pavimento dell’aula giudiziaria e cercare di capire cosa presuppongono davvero quei giuramenti; insomma, ciò che tacitamente implicano quelle formule processuali.



Il principio più importante che presuppongono è l’esistenza della verità; al tempo stesso ne danno per scontata anche la conoscibilità, che non è un presupposto da poco, e sembra indiscussa anche la presunzione dell’unicità della verità.

Quest’ultimo punto è quello che le mode giornalistiche sembrano mettere più facilmente in discussione: se facessimo una ricerca su quali aggettivi accompagnino più spesso il sostantivo “verità” nelle comunicazioni di massa, è molto probabile che si troverebbero ai primi posti tutti i componenti della famiglia degli aggettivi possessivi: “la mia verità”, “la sua verità”, la verità di Tizio che contrasta la verità di Sempronio. Immaginiamo che espressioni d’effetto come queste risultino irritanti ai professionisti del diritto, oltre che a gran parte della gente comune: la logica usata nella vita quotidiana resta pur sempre quella (tutto sommato benemerita) di Aristotele, e nei tribunali sembra regnare indiscusso il caro vecchio principio del Terzo Escluso: una cosa è vera o non è vera, senza via di mezzo; quindi la Verità, quella con la maiuscola, è unica. Di conseguenza, se le verità di Tizio e di Sempronio discordano, c’è poco da fare: uno di loro (o entrambi), o mente o sbaglia, e le due contrastanti verità non sono tali, con buona pace dei giornalisti.

Verità giudiziaria e senso comune

Forse è necessario circoscrivere almeno un po’ l’argomento: “verità” è uno di quei termini troppo evocativi, e il suo significato cambia molto in funzione del contesto. Quello giuridico è, tutto sommato, quello forse più vicino al significato comune: si riferisce a eventi del mondo fisico, avvenimenti da appurare, e si limita essenzialmente al tentativo di ricostruire nel modo più realistico possibile ciò che è realmente accaduto. Altri significati più ampi e poetici, come quelli di natura religiosa, non possono essere soggetti a nessuna indagine logica: la frase «io sono la Via, la Verità e la Vita» per molte persone è estremamente significativa, ma la sua validità è del tutto legata a un approccio fideistico, non razionale; e un approccio simile non è analizzabile per definizione.

In un processo giudiziario la ricerca della verità si basa invece proprio sull’analisi dei fatti, ma la mera ricostruzione degli eventi, anche quando ottenuta con ragionevole precisione, non è sufficiente al raggiungimento di una sentenza: occorre anche stabilire quali fossero i moventi, le emozioni e le intenzioni delle parti in causa. Raggiungere un risultato “veritiero” anche di questi aspetti è molto complicato, perché non esiste un metodo certo, né uno strumento oggettivo, né una scala di valori assoluta per misurare le emozioni e le intenzioni degli esseri umani. È per questo che ancora oggi, per valutare aspetti così cruciali, si finisce quasi sempre per affidarsi agli stessi metodi in vigore fin dall’alba dei tempi: si ricorre al giudizio di gruppi di esseri umani ritenuti degni di fede e dotati di raziocinio, come i giudici e le giurie. E che il loro sia un compito assai difficile non ha bisogno d’essere dimostrato, ma ci sono alcuni esperimenti mentali particolarmente illuminanti.



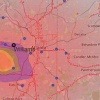
Per illustrare la difficoltà del grado di fiducia da dare alle testimonianze, si può utilizzare una celebre illusione ottica, la scacchiera di Adelson (si veda la figura in alto). Supponiamo che, chiamati a testimoniare di fronte alla corte, Tizio e Sempronio abbiano giurato di non aver mai visto prima la figura e che debbano descrivere i colori delle caselle che nell’immagine sono marcate con le lettere A e B. Come deve comportarsi il giudice se Tizio afferma che la casella A è più scura della casella B, mentre Sempronio afferma che entrambe le caselle sono dello stesso colore?

Se il giudice non conosce l’immagine, probabilmente non avrà dubbi: la differenza dei colori delle due caselle è evidente, quindi Sempronio mente o sbaglia. Se invece la conosce, si troverà in ambasce: sa che le due caselle della scacchiera sono assolutamente della medesima tonalità di grigio (per chi non conoscesse questa famosa illusione: vi assicuriamo che è proprio così, A e B sono dello stesso colore; online si trovano decine di dimostrazioni, oltre che misurazioni con strumenti in grado di classificare i colori) e quindi comincerà a interrogarsi. Sempronio ha mentito quando ha detto di non aver mai visto prima l’immagine? È giusto partire dal presupposto che Tizio sia convinto di aver detto la verità, pur sbagliando, visto che la quasi totalità degli esseri umani risponderebbero che le due caselle sono di colore diverso? Insomma, è più giusto credere a Tizio perché la stragrande maggioranza delle persone avrebbe risposto come lui, oppure a Sempronio, la cui affermazione risponde alla realtà dei fatti?

Dal punto di vista della determinazione delle intenzioni e della correttezza morale di un imputato, può essere significativo uno dei più famosi test di psicologia, il cosiddetto “problema del carrello ferroviario” (trolley problem). Immaginate di trovarvi nei pressi di uno scambio ferroviario, e che un pesante carrello fuori controllo stia per investire cinque persone legate e immobilizzate sui binari: avete solo il tempo di azionare lo scambio deviando la corsa del carrello, ma se lo fate il carrello investirà una persona legata sul binario dove finirà il carrello dopo la deviazione. Il problema nasce come test puramente psicologico, e l’intenzione è solo quella di capire se chi è sottoposto al test preferisce salvare cinque persone assumendosi la responsabilità oggettiva di farne morire una sesta, che senza il suo intervento sopravviverebbe, o se preferisce non assumersi quella responsabilità e non intervenire affatto, anche se questo comporta la morte di più persone. Presupposto del test psicologico è che la persona può decidere se azionare lo scambio o meno senza conseguenze penali, ma solo quelle morali dettate dalla sua coscienza: ma se invece la scena fosse osservata da testimoni e ricostruita in un processo, come dovrebbero comportarsi i giudici? Sarebbe corretto condannare il tapino per omissione di soccorso verso le cinque persone legate, se decidesse di non fare nulla? Sarebbe giusto accusarlo di omicidio, pur con le attenuanti del caso, se invece azionasse lo scambio?

Infine, per quel che riguarda l’identificazione stessa del reato, c’è un famoso indovinello che immagina che tre persone, chiamiamole A, B e C, decidano di fare una traversata di un deserto. Sia A che B sono intenzionate ad assassinare C, ma nessuno è a conoscenza delle intenzioni dell’altro. Una notte, A riesce a versare del veleno nella borraccia di C; poco più tardi, B si intrufola nella tenda di C e gli fora la borraccia, per fare in modo che all’indomani C finisca con il morire di sete. Ed è quello che accade; nei giorni seguenti si apre l’indagine e A e B finiscono sotto processo. È del tutto evidente che C è stato assassinato, ma l’avvocato di A tuona nell’arringa che è pazzesco che il suo cliente sia accusato di omicidio, visto che la vittima non ha bevuto neppure una goccia del veleno che A aveva versato nella sua borraccia. Gli fa eco l’avvocato di B, che con altrettanta veemenza fa notare che l’azione del suo cliente ha solo evitato che C bevesse il veleno, e non è davvero concepibile che impedire a qualcuno di avvelenarsi possa essere considerato un delitto. Come dovrebbe comportarsi il povero giudice?

Verità giudiziaria e verità matematica: una somiglianza imprevista

Tutti questi sono solo giochini, e immaginiamo che i professionisti del diritto potrebbero perfino arrabbiarsi nel veder ridotta l’immensa mole dei principi giuridici a indovinelli da proporre a una cena fra amici. Lungi dal voler sminuire la complessità e l’importanza degli impianti giuridici di tutte le nazioni civili, in realtà l’intenzione è quella di mostrare, almeno in parte, quanto sia complesso raggiungere la verità giudiziaria. I processi si concludono in genere con una sentenza che, prima ancora di stabilire assoluzioni o entità delle pene, deve riassumere cosa è stato giuridicamente appurato dei fatti per i quali si è andati a giudizio. In altri termini, deve riepilogare cosa è vero e cosa non lo è di tutto quanto discusso nel processo.

A dirla tutta, il termine “verità giudiziaria” viene spesso usato proprio per sottolineare la distanza tra l’esito di un processo e quella che è da molti considerata la “verità vera”, quando la sentenza è ritenuta insoddisfacente da un gran numero di persone, e questo anche nel caso in cui, come è richiesto in tutti gli stati giuridicamente evoluti, quella verità giudiziaria sia stata confermata da tre diversi gradi di giudizio. È un destino diametralmente opposto a quello riservato a un altro tipo di verità, certo meno comune, ma talvolta evocata come esempio di certezza inappellabile, incontestabile, assoluta: la “verità matematica”. Se qualcosa è matematicamente certo, allora è inutile dibattere.

Così, se la verità che emerge da un processo è spesso considerata insoddisfacente, quella che deriva da un calcolo matematico è ritenuta assoluta: la differenza di considerazione è insomma assai profonda. Certo, la differenza principale tra i due procedimenti è tanto grande ed evidente da oscurare tutto il resto: l’obiettivo della sequenza di azioni (un processo, appunto) che conduce alla verità giudiziaria è la ricostruzione quanto più possibile esatta di specifici eventi del mondo fisico e del ruolo che in questi eventi hanno avuto delle persone, e infine di decidere se alcune azioni hanno violato delle leggi in vigore e perciò di stabilire delle pene. I procedimenti della matematica, per contro, si disinteressano del tutto del mondo fisico e ancor più delle persone; ma anche se è indubbio che le due verità scaturiscono da procedimenti assai diversi, questo non dovrebbe impedire di notare che tra esse sussistano profonde somiglianze. Anche se i giudici non fanno altro che cercare la verità mentre i matematici, almeno in linea di principio, della verità non sanno proprio cosa farsene.



Non è sempre stato così: i seguaci della scuola pitagorica erano convinti che il Numero fosse davvero l’elemento fondante dell’universo fisico, e gran parte dei filosofi antichi, da Platone fino a Keplero e oltre, cercavano accanitamente (e spesso credevano di aver trovato) in alcune strutture matematiche tutto l’impianto giustificativo della realtà. Ma, speculazioni filosofiche a parte, resta evidente che, per la matematica, la verità non è il riconoscimento dell’immanenza nel mondo di qualcosa che esiste così come viene pensato e descritto, ma solo la constatazione che una certa affermazione è coerente ad alcuni presupposti precedentemente concordati. La verità, nel senso comune del termine, è delegata dalla matematica a quei presupposti che i matematici chiamano postulati.

Ma che i postulati siano veri o meno, tutto sommato, alla matematica interessa assai poco. Quello che conta è la coerenza interna: certo, gli antichi matematici greci, in particolare, cercavano di porre come assiomi delle proposizioni che potessero essere riconosciute come evidenti da tutti; ma ben presto, per salvaguardare la generalità delle conclusioni aritmetiche e geometriche che raggiungevano con le loro dimostrazioni, si ritrovarono a dover qualificare come oggetti matematici enti del tutto inesistenti nel mondo fisico, come linee senza spessore, punti che “non hanno parti” e così via, decretando fin dalla nascita della matematica occidentale la separazione della loro disciplina dalla realtà.

La cosa curiosa è che, con un simile approccio, ogni enunciato matematico sembra ridursi a tautologia, perché derivato, più o meno direttamente, da una serie di assiomi: se un’affermazione è coerente con i postulati non solo è “vera”, ma è anche inevitabile, implicita negli assiomi stessi. Da questo punto di vista, i testi di matematica sembrano ridursi a una serie di istruzioni e regolamenti su quali siano i metodi corretti per utilizzare i postulati inizialmente stabiliti. È qui che sorprendentemente compare una stretta relazione con il diritto: dei Quattro Codici, i testi guida della giurisprudenza, due elencano le leggi e le pene, ma gli altri due scandagliano con puntigliosa precisione quali debbano essere i procedimenti per raggiungere un giudizio. I Codici di Procedura civile e penale sono la vera essenza del diritto: mettono sullo stesso piano d'importanza sia la “verità” sia le regole da seguire per raggiungerla. Ed è cosa fondamentale: anche se talvolta capita che il grande pubblico si irriti quando la prova chiave di un processo non viene ammessa perché ottenuta in maniera impropria, o che un processo intero venga annullato per qualche misterioso “vizio di forma”, è proprio il rispetto delle regole procedurali ciò che garantisce l’equità del processo. E, almeno da un certo punto di vista, tutta la matematica non è altro che un gigantesco codice di procedura che si preoccupa della correttezza del pensiero, e si disinteressa della realtà.

Alla ricerca della verità matematica (se esiste)

Sembra tutto perfetto, vero? Armati di assiomi appropriati e del metodo dimostrativo tanto caro agli antichi Greci possiamo giocare a trovare proprietà strabilianti, meravigliosamente inattese eppure tutte già contenute in pochi principi che tutti gli esseri umani sono pronti ad accettare. L’unico rischio è quello di annoiarsi, una volta che ogni possibile conseguenza derivabile dai postulati sia stata sviscerata: ma, come ricordava Amleto, ci sono più cose in cielo e in terra di quante ne possa immaginare la nostra filosofia. La noia non fa in tempo a comparire perché arrivano subito i guai. Forse è solo una leggenda che i Pitagorici abbiano messo a morte Ippaso di Metaponto perché rivelò l’esistenza dei numeri irrazionali, ma è significativa ugualmente: il Numero adorato da quella scuola filosofica è solo quello intero o dato dal rapporto di numeri interi, e se esistono grandezze che non sono esprimibili così, allora non è vero che «tutto è numero». A meno di cambiare la definizione di numero, ovviamente. Zenone di Elea tormenta i colleghi filosofi con quei suoi giochetti che tirano in ballo l’infinito, e i suoi colleghi di sicuro si spazientiscono, come del resto farà anche Newton quando Berkeley irriderà i suoi infinitesimi come «fantasmi di quantità defunte», ma i semi del dubbio sono ormai piantati, e prima o poi germoglieranno.

Comincia presto a serpeggiare l’idea che forse alcuni assiomi meritano di essere rivisti, o almeno meglio precisati: dopo tutto, le convenzioni umane — e per quanto nobili, i postulati della matematica questo sono — possono cambiare. Anzi, lo fanno continuamente, e certe volte lo facciamo quasi inconsapevolmente: siamo tutti convinti che 2+2=4 e ci dimentichiamo che questa inattaccabile verità discende da qualche postulato che risale al concetto di “successore” nella sequenza dei numeri naturali, e a un certo numero di convenzioni simboliche e proprietà dedotte fin dall’alba dei tempi. Con la medesima logica possiamo affermare senza tema d’essere contraddetti che 9+8+1 fa 18, e che qualsiasi risultato diverso sia legittimo etichettarlo come “falso”, anche se quasi sempre, di fatto, pensiamo che il risultato sia 6, quando abbiamo lavorato per otto ore dopo essere entrati in ufficio alle nove e fatto un’ora di pausa per il pranzo. Siamo passati agli assiomi dell’aritmetica modulare in base 12, ma ci è così familiare che non ce ne siamo resi conto.

Con buona pace dei Pitagorici, adesso consideriamo “numeri” anche quelli che per loro numeri non erano, alcuni dei quali sono veramente strani: esistono (o “abbiamo inventato”, anche questa è una questione aperta da secoli) numeri per i quali 3x4 dà un risultato diverso da 4x3; numeri che sono sparpagliati su un piano, per i quali non esiste un ordinamento che ci consenta di dire se uno sia più grande o più piccolo di un altro. Basta cambiare postulati, e se si è fortunati si possono scoprire altri universi densi di verità diverse: per due millenni le migliori menti matematiche del pianeta si sono sforzate di spiegare a Euclide che uno dei suoi postulati della geometria, il Quinto, era talmente strano e insolito che doveva per forza essere dimostrabile: era insomma un teorema, e non c’era bisogno di farlo assurgere alla somma dignità di postulato. È poi finita che invece aveva ragione Euclide: quello era proprio un postulato, e quando qualcuno ha provato a cambiarlo la geometria euclidea ha perso la sua unicità (e con essa gran parte della sua fama di “verità”), ma in cambio abbiamo ottenuto un’infinità di altre geometrie, e va a sapere adesso quale sia tra queste quella che meglio descrive le caratteristiche di questo nostro universo.



Però i logici, lo abbiamo già detto, sono i più tignosi fra i matematici, e non hanno mollato la presa: i processi matematici sono così meravigliosamente logici che sembrava impossibile che la matematica tutta non potesse essere del tutto ricondotta alla logica e ai suoi assiomi caratteristici. Ci prova anche Peano, convinto che il primo passo fondamentale per raggiungere l’obiettivo sia quello di cambiare il linguaggio, e si mette a inventare una lingua nuova; ma a provarci più seriamente di tutti è forse Gottlob Frege, che passa la vita a scrivere un’opera monumentale sui principi dell’aritmetica, per essere poi gettato nella disperazione dalla fugace osservazione di un giovane Bertrand Russell. Questi ne raccoglie comunque il testimone, e prova a correggere il mastodontico edificio della matematica costruita su basi logiche insieme a Whitehead; edificio che crolla per colpa proprio di quel Kurt Gödel che abbiamo incontrato qualche pagina fa, che da dietro i suoi tondi occhialini fa notare al mondo che non esiste solo il vero e il falso, ma qualcosa che non è né l’uno né l’altro.

Non si tratta di mancanza di informazioni, di qualcosa che non sappiamo se sia vero o falso perché ci mancano conoscenze cruciali per capirlo, ma proprio dell’esistenza di qualcosa di indecidibile per natura. Vanno a farsi benedire il principio aristotelico del Terzo Escluso, l’ipotesi da sempre sottointesa della conoscibilità della verità e ovviamente anche l’illusione della sua unicità. Anzi, tanto per completare l’opera distruttiva, arriva anche Alfred Tarski che è probabilmente il logico che più a fondo ha studiato il concetto di verità, e i cui risultati non sono certo riassumibili in una frase ad effetto: se proprio dovessimo inventarcene una per riassumere il suo pensiero, diremmo che realtà e verità non hanno niente da spartire, ma sarebbe certo un logico peccato mortale se pensassimo davvero di essercela cavata così.

Ma il guaio vero è provare a estrarre una qualsiasi conclusione in merito alla questione centrale affrontata in questo articolo: se la matematica è un insieme di infinite matematiche, e se la verità probabilmente non esiste, come si può provare a stabilire un rapporto tra i due concetti? Per nostra fortuna, che sia vera o meno, la matematica resta comunque sorprendente e meravigliosa.